Chapter 1
Relationships
1.5 The Algebra of Functions
1.5.5 Symbolic Representation of Inverse Functions
Inversion of functions has a standard notation, one that you have probably already used in connection with inverse trigonometric and inverse logarithmic functions: The symbol `f^-1` represents the inverse of the function `f`. We hasten to add that you must interpret this notation with care: It looks like it ought to mean `1 text[/] f`, but it clearly does not. After all, the squaring and the square root functions are not reciprocals of each other.
- If `ftext[(]x text[)]=x^2`, what function is `1 text[/] f`?
- If `ftext[(]x text[)]=sqrtx`, what function is `1 text[/] f`?
- If `ftext[(]x text[)]=x^3`, what function is `1 text[/] f`?
- If `ftext[(]x text[)]=x^3`, what function is `f^-1`?
- Let `ftext[(]x text[)]=x^3`. Draw the graphs of `f`, `1 text[/] f`, and `f^-1`. (Use your graphing tool — computer or calculator.) Explain the features of the three graphs that tell you which goes with each function.
Example 3
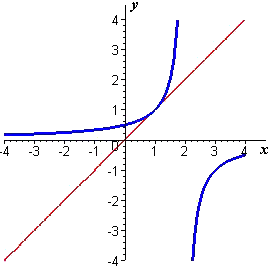
Figure 9 Graph of f(x) = 1/(2 - x)
Figure 9 shows the graph of `ftext[(]x text[)]=1 text[/(]2-xtext[)]` (blue curve). What is the inverse relation? Is it a function? What is a formula for this function?
Solution
In principle, all we have to do is flip the graph of `ftext[(]x text[)]` over the graph of `y=x` (red line in Figure 9), and we will have a graph of the inverse relation. This will help you answer the first two questions, but it won't help with the third. For that, we need to do some algebra.
First, the graph of `f` is also the graph of the equation `y=1 text[/(]2-xtext[).]` If we interchange the variables and in this equation, we get
`x=1/(2-y)` ,
which is an equation that defines the inverse relation — but it does not tell us how to express `y` as a function of `x`. For that, we need to solve the equation for `y`. We begin by taking reciprocals on both sides:
`1/x=2-y`.
Then we add `y` to both sides:
`y+1/x=2`.
Now we may solve for `y` by subtracting `1/x` from both sides:
`y=2-1/x`.
This last equation shows us that the inverse relation is indeed a function — each `x` determines a unique `y` — ![]() and it also gives us a formula for `f^-1`.
and it also gives us a formula for `f^-1`.
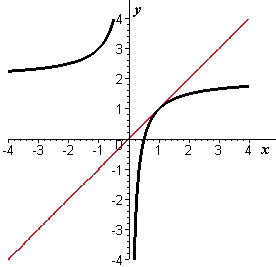
We graph this inverse function in Figure 10. In case there is any doubt about whether this is the reflection of the graph of `f` around the line `y=x`, in Figure 11 we show both graphs, `f` with a blue line and `f^-1` with a black line.
 |
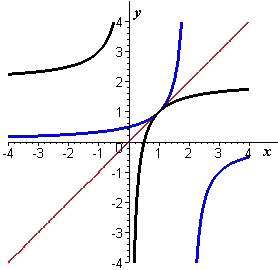 |
Figure 10 Graph of f -1(x) = 2 - 1/x |
Figure 11 Combined graphs of f and f -1 |



