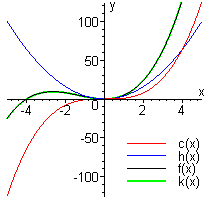
Figure A1 The function f as
a sum of simpler functions
a sum of simpler functions
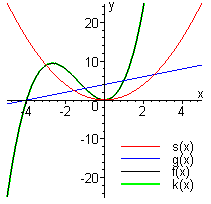
Figure A2 The function f as
a product of simpler functions
a product of simpler functions
One way to express `f` in terms of operations on simpler functions is to write it as the sum of the cubing function `ctext[(]x text[)]=x^3` and the quadratic function `htext[(]x text[)]=4x^2`. See Figure A1, in which `k` is the sum of `c` and `h`.
Another possibility is to write `f` as a product: `ftext[(]x text[)]=stext[(]x text[)] gtext[(]x text[)]`, where `stext[(]x text[)]=x^2` and `gtext[(]x text[)]=x+4`. See Figure A2, in which `k` is the product of `s` and `g`. Note that the vertical scales are different in the two figures — the black and green graphs represent the same function in both graphs.
 |
 |
|---|---|
Figure A1 The function f as a sum of simpler functions |
Figure A2 The function f as a product of simpler functions |