We show the graph of the function `text[(]x^3-8text[)/(]x-2text[)]` in Figure A1. It looks remarkably like the graph of a quadratic polynomial, and you may have noticed that `x-2` divides evenly into `x^3-8`. In fact, except at `x=2`, `text[(]x^3-8text[)/(]x-2text[)] = x^2 + 2x + 4`.

The graph is missing the point at `text[(]2,12text[)]`, but there can be little doubt that the function values are close to `12` when `x` is close to `2`. Thus,
`lim_(x rarr 2) (x^3 - 8)/(x - 2) = lim_(x rarr 2) (x^2 + 2x + 4) = 12`.
You also might have looked at this as a derivative calculation for a well-known function, `f text[(] x text[)] = x^3`:
`f' text[(] 2 text[)] = lim_(x rarr 2) (ftext[(] x text[)]-ftext[(] 2 text[)])/(x-2) = lim_(x rarr 2) (x^3 - 8)/(x - 2)`.
But `f' text[(] 2 text[)] = 3 times 2^2 = 12`, which is another way to get the same answer.
Our second function is also a difference quotient for a well-known function, but that may not be evident until you write the quotient in another form:
where `g text[(] t text[)] = ln t` and `x = Delta t`. Thus the limiting value is `g' text[(] 2 text[)] = 1text[/]2`. We show a graph of the given function in Figure A2.
Similarly, if we take `h text[(] x text[)] = cos x`, then we know that `h' text[(] x text[)] = -sin x` so `h' text[(] 0 text[)] = 0`. On the other hand, if we calculate the derivative at `0` by difference quotients, we find
If the negative of our answer is `0`, so is the answer itself. We show the graph of the function `text[(]1 - cos xtext[)/]x` in Figure A3.
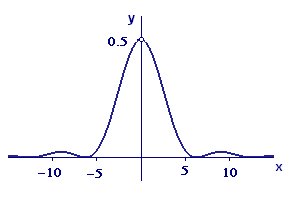
We don't want to give the impression that all interesting limiting value calculations are just derivatives in disguise. Part (d) of Activity 3 is a case in point. It is easy to determine — for example, by tracing the graph — that
`lim_(x rarr 0) (1 - cos x)/x^2 = 1/2 `.
It's not at all easy to explain why — not yet. Later in this chapter this will be a relatively easy calculation. There we will see that we can represent `cos x` by a formula of the form
`cos x = 1 - 1/2 x^2 +`other terms with higher powers of `x`.
When we subtract this expression from `1` and divide by `x^2`, we are left with
`(1 - cos x)/x^2 = 1/2 +`other terms with factors of `x`.
When we let `x rarr 0` all that is left is the constant term, `1//2`. We show a graph of the relevant function in Figure A4.