Chapter 10
Polynomial and Series Representations of Functions





10.2 Approximation of Functions: Taylor Polynomials

10.2.2 Taylor Polynomials for `e^x`

We now give a name to the approximating polynomials we constructed on the preceding page.

Definition   The Taylor polynomials for a function `f text[(] x text[)]` at the reference point `x = 0` are the polynomials of the form
P n ( x ) = f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) 2 x 2 + ⋅⋅⋅ + f ( n ) n ! x n .

In sigma notation, we may write the defining formula as
P n ( x ) = ∑ k = 0 n f ( k ) ( 0 ) k ! x k .

A note about the terminology: The Taylor polynomials at `0` are also called Maclaurin polynomials for `f text[(] x text[)]`. We will not use this terminology because one name is enough, because we will have occasional need for Taylor polynomials at other reference points, and because computer programs that know about these polynomials generally use "Taylor."

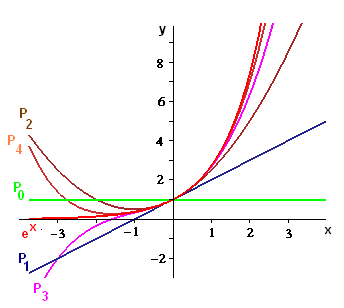
In Figure 1 we plot the graphs of the exponential function and its first five approximating Taylor polynomials. [This figure is repeated from the Answer to Checkpoint 2 on the preceding page.]

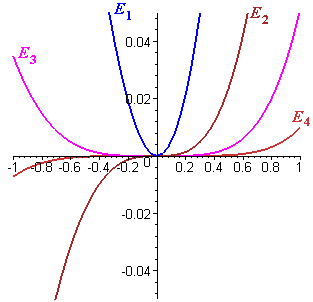
Figure 1   Exponential function `e^x` and Taylor polynomials up to degree `4`

In Figure 2 we plot the errors in the polynomial approximations, i.e., the functions `E_n text[(] x text[)] = e^x - P_n text[(] x text[)]`, up to `n = 4`. Notice the change of scale from Figure 1: In the error plot we consider only the interval from `x = -1` to `x=1,` and we have exaggerated the vertical scale to make the errors show up. Thus we can see clearly, for example, that `P_1 text[(] x text[)]` moves quickly away from the exponential curve for values of `x` not very far from zero, but `P_4 text[(] x text[)]` stays within `0.01` of `e^x` over the entire interval from `-1` to `1`.

Figure 2   Errors `E_ntext[(] x text[)] = e^x - P_ntext[(] x text[)]` in Taylor polynomial approximations to `e^x` up to degree `4`

Notice the shapes of the graphs in Figure 2: The error in the linear approximation looks quadratic, the error in the quadratic approximation looks cubic, and so on. There is a good reason for this. The quadratic approximation, for example, has been selected to exactly match the quadratic part of the exponential function — which will have a precise meaning when we represent `e^x` as a "very long polynomial." When that quadratic part is subtracted from `e^x`, what is left of the very long polynomial is the part of degree `3` and higher — and the cubic part dominates all the rest.

Go to Back One Page Go Forward One Page

Contents for Chapter 10