Exercises

1. 1. If `f text[(] x text[)]=sin x`, what is the coefficient of `x^5` in the seventh-degree polynomial approximation `P_7 text[(] x text[)]` of `f text[(] x text[)]`?
   2. For any function `f text[(] x text[)]` with enough derivatives, what is the coefficient of `x^5` in the seventh-degree polynomial approximation `P_7 text[(] x text[)]` of `f text[(] x text[)]`?
   3. For any function `f text[(] x text[)]` with enough derivatives and any positive integers `k` and `n` (`n>=k`), what is the coefficient of `x^k` in the
      `n`^th-degree polynomial approximation `P_n text[(] x text[)]` of `f text[(] x text[)]`?
2. What is the
   1. seventh-degree Taylor polynomial approximation to `f text[(] x text[)]=sin x text[?]`
   2. fourth-degree Taylor polynomial approximation to `g text[(] x text[)]=cos x`?
   3. sixth-degree Taylor polynomial approximation to `h text[(] x text[)]=e^x`?
3. Figure E1 shows a possible response to Activity 2(c).
   1. Why are only three error curves plotted in Figure E1?
   2. Interpret each of the curves in Figure E1 as we did for the exponential function. What can you say about their shapes?
   3. For approximately what interval does the cubic approximation to the sine function match `sin x` to within `0.01`?

   
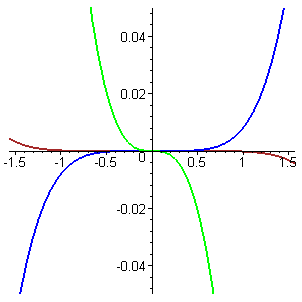
   Figure E1  Error curves for Taylor polynomials for `f text[(] x text[)]=sin x` up to degree 5

4. 1. What is the largest error (in absolute value) in the fifth-degree approximation to the sine function over the entire interval `[-pitext[/]2,pitext[/]2]`?
   2. For what `x`'s does that largest error occur?
   3. For each such `x`, is `sin x`  larger than or smaller than `P_5 text[(] x text[)]`?
5. You may want to adapt your graphing tool from Activity 2 for this exercise.

   1. Find the Taylor polynomials of degrees `0` through `6` for the function `f text[(] x text[)]=cos x`.
   2. In a single plotting window, graph `f text[(] x text[)]=cos x` and the Taylor polynomials you calculated in part (a).
   3. In a single plotting window, graph the errors in the Taylor polynomials you calculated in part (b).
   4. Interpret each of the error curves as we did for the exponential function. What can you say about their shapes?
   5. For approximately what interval does the sixth-degree approximation to the cosine function match `cos x` to within `0.01?`
6. 1. What is the largest error (in absolute value) in the sixth-degree approximation to the cosine function over the entire interval `[-pitext[/]2,pitext[/]2]?`
   2. For what `x`'s does that largest error occur?
   3. For each such `x`, is `cos x`  larger than or smaller than `P_6 text[(] x text[)]`?
7. 1. What calculus operation, when applied to `sin x`, gives `cos x`?
   2. What happens if you perform the same operation on the Taylor polynomials for `sin x`?
   3. What happens if you differentiate the Taylor polynomials for `e^x`?
   4. Is your answer to part (c) consistent with your answer to part (b)?
8. 1. Calculate `e` (`=e^1`) by substituting `x=1` into the appropriate polynomials `P_n text[(] x text[)]` for `e^x` with increasing values of `n` until you see no change in the sixth decimal place. [Hint: `P_ntext[(]1text[)]=P_(n-1)text[(]1text[)]+1text[/]n!` for every value of `n`, so you can get each new approximation by adding a single term to the preceding one.]
   2. Check your result in part (a) by comparing your partial sums with your computer's or calculator's value for `e`.
9. 1. Calculate `sin 1` (radian) by substituting `x=1` into the appropriate polynomials `P_n text[(] x text[)]` with increasing values of `n` until you see no change in the sixth decimal place.
   2. Check your result in part (a) by comparing your partial sums with your computer's or calculator's value for `sin 1`.
10. 1. Calculate `cos 1` (radian) by substituting `x=1` into the appropriate polynomials `P_n text[(] x text[)]` with increasing values of `n` until you see no change in the sixth decimal place.
    2. Check your result in part (a) by comparing your partial sums with your computer's or calculator's value for `cos 1`.
11. 1. Here, courtesy of a computer algebra system, are a well-known function and its first five derivatives:

       `f text[(] x text[)]`	`=tan x`
       `f' text[(] x text[)]`	`=1+tan^2 x`
       `f'' text[(] x text[)]`	`=2 tan x+2 tan^3 x`
       `f^((3)) text[(] x text[)]`	`=2 +8 tan^2 x+6 tan^4 x`
       `f^((4)) text[(] x text[)]`	`=16 tan x +40 tan^3 x+24 tan^5 x`
       `f^((5)) text[(] x text[)]`	`=16+136 tan^2 x +240 tan^4 x+120 tan^6 x`

       Find the fifth-degree Taylor approximation `P_5 text[(] x text[)]` to `f text[(] x text[)]`.
    2. Use your graphing tool (or adapt one of ours) to find an interval over which the graph of `P_5 text[(] x text[)]` appears to fit the graph of `f text[(] x text[)]` well.
    3. Using an appropriate `y`-scale, graph `f text[(] x text[)]-P_5 text[(] x text[)]` on the interval you determined in part (b), and find the maximum error in the approximation on that interval.
12. With your graphing tool, graph `e^x` and `1+x` for `-2<=x<=2` and `-5<=y<=5`. One term at a time, change the second function to higher degree Taylor polynomial approximations for `e^x`, and regraph. That is, first add `x^2`/`2`, then `x^3`/`6`, and so on. As the Taylor approximation begins to look very close to `e^x`, enlarge the window so you can see clearly how and where the two functions differ. Continue up to at least degree `5`. Describe in your own words the characteristics that distinguish all the Taylor polynomials from `e^x`.
13. With your graphing tool, graph the functions `e^x- text[(] 1+x text[)]` and `x^2`/`2`. That is, graph the error in the approximation of `e^x` by `1+x`, as well as the first term "left out" of the approximation. Set the window at `-1<=x<=1` and `-1<=y<=1` with tick marks on both axes at a spacing of `0.1`. If your tool has a grid option, turn it on.
1. What is the approximate shape of the error curve?
2. For what values of `x` is the error smaller (in absolute value) than the next term?
3. For what values of `x` is the error larger (in absolute value) than the next term?
4. What is the largest error (in absolute value) on the interval `[-1,1]`, and where does this largest error occur?
5. In what interval on the `x`-axis is |error| no larger than the distance between `y` tick marks?
6. Now make the first function `e^x-text[(]1+x+x^2text[/]2text[)]` and the second function `x^3text[/]6`. Change the `y`-range to `[-0.25,0.25]` with tick marks on the `y`-axis at a spacing of `0.025`. Answer the same questions as in parts (a)–(e). Record your numerical results in a table like the one shown in Table E1.

   Table E1   Errors in polynomial approximations to `e^x`

   Degree	Max y	y tick spacing	Max |error| on [-1,1]	Interval for |error| `<=` tick spacing
   1	1.0	0.1	0.72	[-0.47,0.41]
   2	0.25	0.025
   3	0.1	0.01
   4	0.01	0.001
   5	0.0025	0.00025
   6	0.00025	0.000025

7. Continue adding terms to the error function and changing the "next term", answering the questions of parts (a)-(e), and filling in each line of Table E1. Use the ranges and tick spacing indicated in the table.
14. Give a reason why each of the following functions is not a polynomial function.
    1. The exponential function
    2. The sine function
    3. The cosine function
    4. The natural logarithm function
    5. The inverse tangent function
    6. The normal probability density function
    7. The error function
15. 1. Find the Taylor polynomials of degrees 0, 1, 2, 3, and 4 that approximate the function `f text[(] x text[)]= 1+x^4 `.
    2. However you answered part (a), there is at least one more way to arrive at the same answer. What's a second way to answer part (a)?
16. 1. Find a fourth-degree polynomial approximation for the function `f text[(] x text[)]=(sin x)/x`. (Hint: Don't calculate any derivatives!)
    2. Graph both `f text[(] x text[)]` and your approximating polynomial.
    3. Use your approximating polynomial to estimate `int_0^1 (sin x)/x dx`.
    4. Use the integral function of your computer or calculator to evaluate the integral in part (c). How accurate was your estimate?
17. 1. Find the first six Taylor polynomial approximations to `f text[(] x text[)]=e^(-x).`
    2. In the first six Taylor polynomials for `g text[(] x text[)]=e^x`, substitute `-x` for `x`. How are the resulting polynomials related to the ones you calculated in part (a)?
    3. Graph `f text[(] x text[)]` and all six of the approximating polynomials in a single graphing window.