10.3.2 Sequences and Series

In ordinary English, the words “sequence” and “series” are synonyms. Each means a list of things, one after another. In mathematics, the two words have different meanings: “Series” carries the meaning of adding the terms of a sequence. Furthermore, both words are used primarily in the context of infinitely long lists.

Definitions   A sequence is an infinitely long list of numbers or expressions. If b 0 , b 1 , b 2 , ... , b k , ... is such a list, we call the sum (with infinitely many terms), b 0 + b 1 + b 2 + ⋅⋅⋅ + b k + ⋅⋅⋅ an infinite series. Often the adjective is dropped, and we call an infinitely long sum a series. As with ordinary addition, the list items `b_k` are called terms of the series. The sum of the first `n+1` terms, b 0 + b 1 + b 2 + ⋅⋅⋅ + b n , is called the `n`th partial sum of the series.

Note carefully the use of the three-dot (ellipsis) notation in these definitions. When an ellipsis occurs between two similar things, it means the pattern on both ends is continued in the middle, and we are just not bothering to fill in all the intervening items. When it occurs at the end of an expression, it means the preceding pattern continues forever.

We observe that the partial sums of a series constitute another sequence:

The terms in this sequence are found by ordinary addition of finitely many terms. If this sequence has a limiting value, we take that value to be the sum of the entire series.

Definitions   If the sequence of partial sums of a series has a finite limiting value `S` we say the series converges, and we call `S` the sum of the series. If the sequence of partial sums does not have a finite limiting value, we say the series diverges.

Example 1

For the series 1 + 1 2 + 1 2 2 + ⋅⋅⋅ + 1 2 k + ⋅⋅⋅ ⁢ , find:

1. the limit of the sequence of terms,

2. the sequence of partial sums, and

3. the sum of the series.

Solution   This is a geometric series with term-to-term ratio `1//2`. The limiting value of the terms is

In Section 10.1 we evaluated the `n`th partial sum of such a series and found that

From this we easily find the sum of the series:

This example is not typical: Geometric series are the only series we have seen for which we know how to find all the partial sums by an explicit formula. For most series of interest, finding the sum — or even determining whether there is a finite sum — will not be so easy.

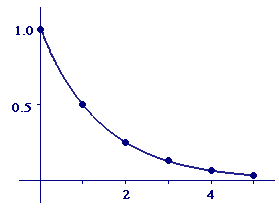
By contrast, finding a limit of the sequence of terms often is easy. In fact, the terms `1, 1/2, 1/4, ..., 1/2^k, ...` of the series in Example 1 are just `ytext[-]`coordinates at integer values of `x` for the function `y=1text[/]2^x`. We illustrate this in Figure 1, which shows both the graph of the function and the points for nonnegative integer values of `x` up to `x=5`. Thus, if you are not sure of a limiting value for terms given by a formula, you can often determine the limiting value by graphing the function defined by the formula. This figure also illustrates that a sequence actually is a special kind of function, namely one whose domain consists of an infinite list of integers.

Checkpoint 1

We will often find it convenient, as we have in earlier chapters, to use sigma notation for the sums — both partial and total — that occur in our study of series. Thus, in Example 1, we could write

for the `n`th partial sum and

for the total sum. In general, a sum with upper limit `oo` is defined by

As usual, whenever you find the sigma notation even a little confusing, we encourage you to write out enough terms explicitly to be sure you understand what the notation represents.