Chapter 10
Polynomial and Series Representations of Functions





10.3 Taylor Series

10.3.3 Taylor Series for `e^x` and `sin x`

In Activity 1 you explored the sequences of numbers of the form

P 0 , P 1 ( x 0 ) , P 2 ( x 0 ) , P 3 ( x 0 ) , P 4 ( x 0 ) ,   ...

where `P_ntext[(]xtext[)]` is the `n`th Taylor polynomial for `e^x,` and `x_0` is any one of your test values. It appeared that each such sequence has `e^(x_0)` as its limit. In fact, Taylor polynomials are partial sums of an infinite series, because each polynomial is the preceding polynomial plus one more term. Specifically, for the exponential function, the terms are the power functions

1 , x , 1 2 x 2 , 1 3 ! x 3 , ... ⁢ ,

and the partial sums are

P n ( x ) = 1 + x + 1 2 x 2 + ⋅⋅⋅ ⁢ + 1 n ! x n = ∑ k = 0 n 1 k ! x k .

We summarize the convergence of these partial sums to `e^x` by writing

e x = 1 + x + 1 2 x 2 + ⋅⋅⋅ ⁢ + 1 k ! x k + ⋅⋅⋅ = ∑ k = 0 ∞ 1 k ! x k .

We have certainly not shown yet that this assertion about limiting values is true — that will come later in the chapter. But we have some graphic and numerical evidence that it is true for a variety of numbers `x_0`. We further illustrate convergence of partial sums with the case of `x = 1` which leads to the following interesting formula for `e`:

e = 1 + 1 + 1 2 + ⋅⋅⋅ ⁢ + 1 k ! + ⋅⋅⋅ = ∑ k = 0 ∞ 1 k ! .

Example 2

Calculate the first ten partial sums of this series representation for `e,` and show that the resulting sequence appears to be approaching `e.`

Solution   Here are the sums:

1 = 1
1 + 1
= 2
1 + 1 + 1 2
= 2.5
1 + 1 + 1 2 + 1 6
= 2.667
1 + 1 + 1 2 + 1 6 + 1 24
= 2.70833
1 + 1 + 1 2 + 1 6 + 1 24 + 1 120
= 2.71667
1 + 1 + 1 2 + 1 6 + 1 24 + 1 120 + 1 720
= 2.718056
1 + 1 + 1 2 + 1 6 + 1 24 + 1 120 + 1 720 + 1 5040
= 2.7182540
1 + 1 + 1 2 + 1 6 + 1 24 + 1 120 + 1 720 + 1 5040 + 1 40320
= 2.71827877
1 + 1 + 1 2 + 1 6 + 1 24 + 1 120 + 1 720 + 1 5040 + 1 40320 + 1 362880
= 2.71828153

The error after adding up `10` terms (i.e., the difference between our last partial sum and `e`) is about `3 times 10^(-7)` — that is, the first six decimal places agree with `e`.

The Taylor polynomials for the sine function create a small problem in that all the even-numbered terms are zero. Specifically, as they were originally derived, the terms are

0 , x , 0 , - 1 3 ! x 3 , 0 , 1 5 ! x 5 , ... ⁢   .

Our record keeping will be simpler if we drop all the zero terms — which contribute nothing to the sum — and renumber the remaining terms by `k = 0, 1, 2, ...`. This makes the degree of the `k`th term `2k + 1`. Thus the `text[(]2n + 1text[)]`th partial sum is

P 2 n + 1 ( x ) = x - 1 3 ! x 3 + 1 5 ! x 5 - ⋅⋅⋅ + ( - 1 ) n ( 2 n + 1 ) ! x 2 n + 1 = ∑ k = 0 n ( - 1 ) k ( 2 k + 1 ) ! x 2 k + 1 .

The corresponding series [the limiting value of `P_(2n+1)text[(]xtext[)]` as `n rarr oo`] is

sin ⁢   x = x - 1 6 x 3 + 1 120 x 5 - ⋅⋅⋅ + ( - 1 ) k ( 2 k + 1 ) ! x 2 k + 1 + ⋅⋅⋅ ⁢   .

In particular, for `x=-pi//2`, the series interpretation is the improbable (but true) formula

- 1 = - π 2 + π 3 6 ⋅ 2 3 - π 5 120 ⋅ 2 5 + ⋅⋅⋅ + ( - 1 ) k + 1 π 2 k + 1 ( 2 k + 1 ) ! ⋅ 2 2 k + 1 + ⋅⋅⋅ ⁢   .

Activity 2

Use your computer or calculator to calculate `sin 1` (radian) by substituting `x = 1` in the series for `sin x` and adding up partial sums until you see no change in the sixth decimal place. Check your result by comparing your partial sums with your tool's value for `sin 1`.

Comment 2Comment on Activity 2

It should come as no surprise that the series whose partial sums are Taylor polynomials are called Taylor series.

Definition   The Taylor series for a function `f text[(] x text[)]` at the reference point `x = 0` is the series
f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) 2 x 2 + ⋅⋅⋅ + f ( k ) ( 0 ) k ! + ⋅⋅⋅ ⁢   .

In sigma notation, we may write the defining formula as

∑ k = 0 ∞ f ( k ) ( 0 ) k ! x k .

Here are the formulas for the Taylor series we know so far. For completeness sake, we include a formula for the cosine function — see Exercise 1.

   e x = 1 + x + 1 2 x 2 + ⋅⋅⋅ + 1 k ! ⁢ x k + ⋅⋅⋅ = ∑ k = 0 ∞ 1 k ! x k
sin ⁢ x = x - 1 6 x 3 + 1 120 x 5 - ⋅⋅⋅ + ( - 1 ) k ( 2 k + 1 ) ! x 2 k + 1 + ⋅⋅⋅ = ∑ k = 0 ∞ ( - 1 ) k ( 2 k + 1 ) ! x 2 k + 1
cos ⁢ x = 1 - 1 2 x 2 + 1 24 x 4 - ⋅⋅⋅ + ( - 1 ) k ( 2 k ) ! x 2 k + ⋅⋅⋅ = ∑ k = 0 ∞ ( - 1 ) k ( 2 k ) ! x 2 k

Example 3

Use the Taylor series for `e^x` to explain why, for any positive integer `m`,

lim x → ∞ x m e x = 0.

That is, show that the exponential function grows much faster than any power function.

Solution   Since the terms in the exponential series are all positive when `x` is positive, `e^x` is bigger than every term of the series. In particular,

e x > 1 ( m + 1 ) ! x m + 1 .

Thus

x m e x < x m x m + 1 ( m + 1 ) ! = ( m + 1 ) ! x .

No matter how big `text[(]m + 1text[)]!` is, it's constant, and `x` will eventually be bigger. Thus

0 ≤ lim x → ∞ x m e x ≤ lim x → ∞ ( m + 1 ) ! x = 0.

end solutionHence the limit must be `0`.

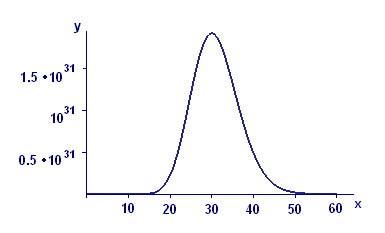
In Figure 2 we illustrate the significance of Example 3 for the case of `m = 30`. Take careful note of the scales in the figure. The function `x^30`/`e^x` peaks at about `x = 30` with a value of about `1.93 times 10^31`. Pretty big! If you started to graph this function without knowing what to look for, you might never guess that this is a function that eventually goes to zero. If you try to produce a comparable picture for `m = 100,` your graphing tool will fail. (Don't take our word for it — try it!) Nevertheless, we can solve problems of such enormous magnitude with relatively simple calculations — and powerful concepts.

Figure 2   Graph of y = x30/ e x
Go to Back One Page Go Forward One Page

Contents for Chapter 10