10.6.3 Convergence of the Logarithmic Series

Here again is the Taylor series for `ln text[(] 1+x text[)]`, with terms renumbered for convenience:

ln ( 1 + x ) = x - x 2 2 + x 3 3 - x 4 4 + ⋅⋅⋅ = ∑ k = 1 ∞ ( - 1 ) k + 1   x k k ,     if ⁢   | x | < 1.

Notice that this series does not have odd symmetry — or any symmetry at all, since every positive power of `x` appears in it. No surprise there — the natural logarithm function doesn't have any symmetry either. This series is alternating for some values of `x`, but not for all.

Activity 2

1. For what values of `x` will the Taylor series for `ln text[(] 1+x text[)]` satisfy all the bulleted conditions of the Alternating Series Test?
2. For what values of `x` does the Alternating Series Test ensure that the Taylor series for `ln text[(] 1+x text[)]` converges? (You already determined one such value of `x` in the preceding section.)
3. For each such `x` and each fixed value of `n`, how big can the error be in the `n`th degree Taylor polynomial approximation to `ln text[(] 1+x text[)]`? In particular, for `x=1//2` and `n=10`, how close must `P_10text[(]1text[/]2text[)]` be to `ln 3//2`? Calculate both `P_10text[(]1text[/]2text[)]` and `ln 3//2` to be sure.
4. Explain why the Taylor series for `lntext[(] 1+x text[)]` must diverge if `text[|] x text[|] >1`.

Comment on Activity 2

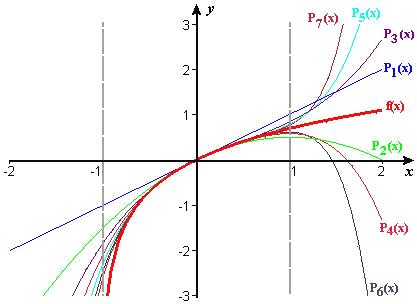
Activity 2 leaves a gap in your knowledge of exactly where the logarithmic series converges — although what happens in that gap is at least suggested by Figures 1 and 2, repeated here from Figures 1 and 2 in Section 10.4. The fact that the series does not always have alternating signs (e.g., at `x=-1//2`) does not tell us that the series diverges there — it merely says that we can't apply the Alternating Series Test to find out.