10.6.4 Using Geometric Series to Estimate Tails:
           Exponential Series

The Alternating Series Test makes it fairly easy to show that some important Taylor series do indeed converge, at least for some values of the input variable. However, several of our important series are not alternating, e.g., the series for `ln text[(] 1+x text[)]` with `x<0` and the series for `e^x` with `x>0`. Furthermore, there are important series whose terms always alternate in sign, but for which it is not yet clear that the terms decrease to zero, e.g., the series for `sin x` and for `cos x` when `x` is large. We develop here another way — based on geometric series — to detect whether such a Taylor series converges. This geometric series method is not particularly sensitive to sign patterns of the terms — in fact, it often works in the worst-case scenario of a series whose terms are all of the same sign.

To illustrate our problem, here again is the Taylor series for the exponential function:

e x = 1 + x + 1 2 ⁢ x 2 + 1 6 ⁢ x 3 + ⋅⋅⋅ + 1 k ! ⁢ x k + 1 ( k + 1 ) ! ⁢ x k + 1 + ⋅⋅⋅ .

Suppose we knew nothing about the origin of this series, and we simply defined a new function `G text[(] x text[)]` by

G ( x ) = 1 + x + 1 2 ⁢ x 2 + 1 6 ⁢ x 3 + ⋅⋅⋅ + 1 k ! ⁢ x k + 1 ( k + 1 ) ! ⁢ x k + 1 + ⋅⋅⋅

for all numbers `x` for which the series converges — no matter what it converges to. `G` is a new function because we have not shown yet that it equals the exponential function. From our graphical studies of the Taylor polynomials for the exponential function, we have some reason to believe that every number `x` may be in the domain of `G` — that's one of the things we will establish in this section. Our immediate task, then, is to determine the domain of the function `G`.

Because we need to get away from Taylor series as the source of all of our examples, we will use the term “power series” to stand for any “infinite polynomial.”

Definitions   A power series in `x` is any expression of the form c 0 + c 1 x + c 2 ⁢ x 2 + c 3 ⁢ x 3 + ⋅⋅⋅ + c k ⁢ x k + ⋅⋅⋅ , or, in sigma notation, of the form ∑ k = 0 ∞ c k x k , where the coefficients `c_0`, `c_1`, `c_2`, and so on, may be any real numbers. We will say that a function `g` is defined by a power series if g ( x ) = c 0 + c 1 x + c 2 ⁢ x 2 + c 3 ⁢ x 3 + ⋅⋅⋅ + c k ⁢ x k + ⋅⋅⋅ .

By convention, the domain of the function `g` consists of all the numbers for which the defining series converges. Thus our function

G ( x ) = 1 + x + 1 2 ⁢ x 2 + 1 6 ⁢ x 3 + ⋅⋅⋅ + 1 k ! ⁢ x k + 1 ( k + 1 ) ! ⁢ x k + 1 + ⋅⋅⋅

is defined by a power series, namely, the Taylor series for the exponential function. We will show in this section that the domain of `G` contains all real numbers and in the next section that `G` really is the exponential function.

Given a power series, the sum of the first `n` terms (the terms numbered from `0` to `n-1`) is

s n = c 0 + c 1 x + c 2 ⁢ x 2 + c 3 ⁢ x 3 + ⋅⋅⋅ + c n - 1 ⁢ x n - 1 .

What's left over — not included in the `n`th partial sum — we call the `n`th tail of the series:

n ⁢ th ⁢     tail = c n x n + c n + 1 ⁢ x n + 1 + c n + 2 ⁢ x n + 2 + c n + 3 ⁢ x n + 3 + ⋅⋅⋅ .

Now the `n`th tail is itself a power series. For a fixed value of `n`, if the `n`th tail converges, then so does the original series, because what's left to be added on, the partial sum `s_n`, is an ordinary sum. To show that the original power series converges, we only have to find an `n` for which the `n`th tail converges.

We recall that, for any numbers `A` and `B`, `|A+B|<=|A|+|B|`. That is, the size of a sum cannot be any bigger than the sum obtained by first taking absolute value of each of the terms — a sum in which no cancellation can occur. The implication for `n`th tails is

| n ⁢ th ⁢     tail | = | c n x n + c n + 1 ⁢ x n + 1 + c n + 2 ⁢ x n + 2 + c n + 3 ⁢ x n + 3 + ⋅⋅⋅ |

≤ | c n |   | x | n + | c n + 1 |   | ⁢ x | n + 1 + | c n + 2 |   | ⁢ x | n + 2 + | c n + 3 |   | ⁢ x | n + 3 + ⋅⋅⋅ .

Thus, if the sum of absolute values is finite, so is the `n`th tail.

Example 2   For any number `x`, show that

G ( x ) = 1 + x + 1 2 ⁢ x 2 + 1 6 ⁢ x 3 + ⋅⋅⋅ + 1 k ! ⁢ x k + 1 ( k + 1 ) ! ⁢ x k + 1 + ⋅⋅⋅

converges.

Solution   For this power series,

n ⁢ th ⁢     tail = x n n ! + ⁢ x n + 1 ( n + 1 ) ! + ⁢ x n + 2 ( n + 2 ) ! + ⋅⋅⋅ .

If this infinite sum converges, it has the same value as the expression we get by factoring out all the common factors, `x^n` in the numerators and `n!` in the denominators:

| n ⁢ th ⁢     tail | = | x n n ! ⁢     [ 1 + ⁢ x ( n + 1 ) + ⁢ x 2 ( n + 1 ) ( n + 2 ) + ⋅⋅⋅ ] |

≤ | x | n n ! ⁢     [ 1 + ⁢ | x | ( n + 1 ) + ⁢ | x | 2 ( n + 1 ) ( n + 2 ) + ⋅⋅⋅ ] .

The value of this last expression is no bigger than the sum we get by replacing each term in the brackets with a term that is at least as large. Our plan will be to replace all the factors `n+2`, `n+3`, and so on, in the denominators of the third and later terms with `n+1`. This gives us the estimate

| n ⁢   th ⁢       tail | ≤ | x | n n ! ⁢     [ 1 + ⁢ | x | n + 1 + ⁢ ( | x | n + 1 ) 2 + ( | x | n + 1 ) 3 + ⋅⋅⋅ ] .

The series inside the brackets is a geometric series `1+r+r^2+r^3+cdots` with term-to-term ratio `r= text[|] x text[|]  text[/]  text[(] n+1 text[)]`. We learned in Section 10.4 all there is to know about convergence of these series. In particular, a geometric series with term-to-term ratio `r` converges if `text[|] r text[|]<1`. Furthermore, when `text[|] r text[|] <1`, the geometric series converges to `1 text[/] text[(] 1-r text[)]`. Thus no matter what `x` is, as soon as `n` is large enough that `text[|] x text[|] text[/] text[(] n+1 text[)] <1`, the tail converges. Now, for any `x` we can find such an `n`, namely, the first integer as big as `text[|] x text[|].` For example, if `x=6.7`, then we can take `n=7`, and `6.8text[/(]7+1text[)]` is certainly less than `1`. This shows that the exponential series which defines `G text[(] x text[)]` converges for every real number `x`.

We turn now to the question of estimating the error in a polynomial approximation, i.e., the error in a partial sum of a power series. For a given value of `x`, if the series happens to converge to the number `S`, then the error after summing `n` terms, `text[|] S-s_n text[|]`, is the absolute value of the `n`th tail. Our job then is to estimate the size of the `n`th tail — essentially the same task we illustrated in Example 2 as a key step in showing that power series converges.

Example 3   Estimate the largest possible error on the interval `-2<=x<=2` if

G ( x ) = 1 + x + 1 2 ⁢ x 2 + 1 6 ⁢ x 3 + ⋅⋅⋅ + 1 k ! ⁢ x k + 1 ( k + 1 ) ! ⁢ x k + 1 + ⋅⋅⋅

is approximated by

P 9 ( x ) = 1 + x + 1 2 ⁢ x 2 + 1 6 ⁢ x 3 + ⋅⋅⋅ + 1 8 ! ⁢ x 8 + 1 9 ! ⁢ x 9 .

Solution   The ninth-degree approximation is the sum of the first 10 terms of `G text[(] x text[)]`, so the error is |10th tail|. In Example 2 we saw that

| n ⁢ th ⁢       tail | ≤ | x | n n ! ⁢     [ 1 + ⁢ | x | ( n + 1 ) + ⁢ | x | 2 ( n + 1 ) ( n + 2 ) + ⋅⋅⋅ ]

= | x | n n ! ⁢     ( 1 + ⁢ r + ⁢ r 2 + r 3 + ⋅⋅⋅ ) , where r = | x | n + 1 ,

= | x | n n !   ( 1 - r ) . ⁢

For this example, `n=10`, `text[|] x text[|] <=2`, and `r<=2//11`. Thus `1-r>=9//11`, and

`|10text(th tail)|<=2^10/(10!text[(]9text[/]11text[)])=0.000344895...<0.0004`.

It follows that any value of `P_9 text[(] x text[)]` for `-2<=x<=2` will approximate `G text[(] x text[)]` to three-decimal-place accuracy.

We haven't established yet that `G` is actually the exponential function, but a computer or calculator tells us that `e^2=7.389056` and `P_9 text[(] 2 text[)] =7.3887125`, so the actual error is about `0.0003436`. In this case, the geometric-series estimate is close to the actual error at the endpoint. On the other hand, `e^-2=0.1353353` and `P_9 text[(] -2 text[)] =0.1350970`, so the actual error is about `0.0002383`. In this case, the error estimate is somewhat conservative. For values of `x` closer to `0`, the actual error will be much smaller than our estimate.

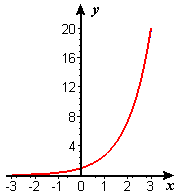
We illustrate this point with Figures 3 and 4, which show, respectively, `e^x` and `P_9 text[(] x text[)` plotted together on the interval `[-3,3]` and the error on the interval `[-2,2]`. You see the graph of only one function in Figure 3 because the two graphs are visually indistinct at the scale shown. Figure 4 proves that the two functions are not identical, but the small size of the error also shows why the graphs in Figure 3 are visually indistinct.

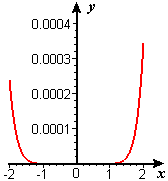Figure 3   Graphs of `e^x` and `P_9text[(] x text[)`	Figure 4   Graph of `e^x-P_9text[(] x text[)`

Checkpoint 2

Figure 4 reminds us that we could have solved the problem in Example 3 with our graphing tool — no algebra needed — provided we knew that `Gtext[(] x text[)]` really is `e^x`. But the algebraic procedure doesn't require that we know the sum of the series — we can estimate error in partial sums without that knowledge, which means we can estimate sums numerically and be sure that we are reasonably close to the right answer. The engineers who designed your computer algebra system or your calculator have to be able to do that in order for it to give you accurate values of the exponential (or any other) function. Furthermore, the algebraic procedure doesn't require that we choose `n` or the interval ahead of time. We explore both of these observations in Exercise 9.

Our estimation of tails of the exponential power series provides a bonus that is important in its own right. For positive values of `x`, the equation

n ⁢ th ⁢     tail = x n n ! ⁢     [ 1 + ⁢ x ( n + 1 ) + ⁢ x 2 ( n + 1 ) ( n + 2 ) + ⋅⋅⋅ ]

shows that the `n`th tail is always larger than `x^n//n!`. We also know that the power series converges, that is,

`lim_(n rarr oo) s_n=S`   or   `lim_(n rarr oo) s_n-S=0`.

But `- text[(] s_n-S text[)] =S-s_n=n`th tail, which is bigger than `x^n//n!`. Now we know what happens to the ratio of `n`th powers to factorials of `n` as `n rarr oo`.

Activity 3

1. Finish the preceding paragraph: For any positive value of `x`, `lim_(n rarr oo) x^n/(n!) =`_______. Finish the explanation as well.
2. Explain why the same conclusion must be true for negative values of `x.`
3. What can you say about the relative growth rates of `10^n` and `n!`, i.e., about the relative sizes of these quantities as `n` becomes large? What about `100^n` and `n!`?

Comment on Activity 3