Problems

You will need graph paper for the first several problems. You can click on the image at the right to get a page from which you can print your own.

In Problems 1-3, `ftext[(]t text[)]` is the reciprocal function, `ftext[(]t text[)]=1/t`.

1. Sketch the graph of `ftext[(]t text[)]`. Check your graph with your graphing tool (computer or calculator).
2. Let `gtext[(]t text[)]` be the difference quotient function for a difference of `Delta t=0.001`:

   `gtext[(]t text[)]=(ftext[(]t+0.001text[)]-ftext[(]t text[)])/0.001`.

   1. Carefully select 8 values of `t`, and calculate the corresponding values of `gtext[(]t text[)]`. (Your careful selection should enable you to sketch the graph of `g`.)
   2. Sketch the graph of `gtext[(]t text[)]`. Check your graph with your graphing tool.
   3. Describe the graph of `gtext[(]t text[)]` in words. For example, you might say how it compares with the graph of `ftext[(]t text[)]`.
3. Graph the derivative of `ftext[(]t text[)]`. How does it compare with the function `g` in Problem 2?

In Problems 4-6, `ftext[(]t text[)]` is the cubing function, `ftext[(]t text[)]=t^3`.

4. Sketch the graph of `ftext[(]t text[)]`. Check your graph with your graphing tool (computer or calculator).
5. Let `gtext[(]t text[)]` be the difference quotient function for a difference of `Delta t=0.001`:

   `gtext[(]t text[)]=(ftext[(]t+0.001text[)]-ftext[(]t text[)])/0.001`.

   1. Carefully select 8 values of `t`, and calculate the corresponding values of `gtext[(]t text[)]`. (Your careful selection should enable you to sketch the graph of `g`.)
   2. Sketch the graph of `gtext[(]t text[)]`. Check your graph with your graphing tool.
   3. Describe the graph of `gtext[(]t text[)]` in words.
6. Graph the derivative of the function `ftext[(]t text[)]=t^3`. How does it compare with the function `g` in Problem 5?
7. Explain why the derivative of `s=3t^2+5` should be `6t`. (See Activity 4.)
8. Suppose gasoline sells for `\$`2.79 a gallon in June and for `\$`3.01 a gallon in July. What can you say about the average price of a gallon of gasoline during those 2 months?
   
   
   Adapted from Calculus Problems for a New Century, edited by Robert Fraga, MAA Notes Number 28, 1993.
9. (See Exercise 17 in Section 1.3.)
   1. What is the rate of change of temperature in degrees Fahrenheit with respect to temperature in degrees Celsius?
   2. What is the rate of change of temperature in degrees Celsius with respect to temperature in degrees Fahrenheit?
   3. What relationship do you observe between these two rates?
10. According to Hooke's Law, the force (weight) required to stretch a spring beyond its natural length (but within its elastic limit) is proportional to the distance stretched. (Click on the image at the right to see a demonstration by Brian Andersson, School of Physics and Astronomy, University of Minnesota. Used by permission.)
    1. Express by a simple formula the force as a function of the distance stretched if a weight of 10 grams stretches a spring 1 centimeter.
    2. For arbitrary weights hung from the same spring (within the elastic limit), what is the rate of change of weight with respect to displacement?
    3. What is the rate of change of displacement with respect to weight?
    4. What relationship do you observe between these two rates?

11. Figure E1 shows successive zoom-ins on the graph of `ftext[(]t text[)]=text[|]t text[|]` in the vicinity of the point `text[(]0,0text[)]`.

    Figure E1   Three views of the absolute value function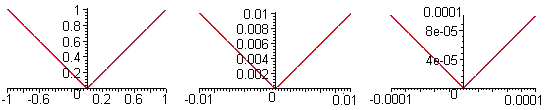

    1. Is this function locally linear at that point? Why or why not?
    2. What is the average slope of the graph from `-Delta t` to `Delta t` for a small value of `Delta t`?
    3. Can you use such an average slope to estimate the rate of change at `t=0`? Why or why not?
    4. What is the average slope of the graph from `0` to `Delta t` for a small value of `Delta t`? From `-Delta t` to `0`?
    5. What do you conclude about instantaneous rate of change at `t=0`?
12. Adapt your computer algebra tool or use the zooming feature on your calculator to zoom in on the graph of `ftext[(]t text[)]=|t^3|` in the vicinity of `text[(]0,0text[)]`.
    1. Is this function locally linear at that point? Why or why not?
    2. What is the average slope of the graph from `-Delta t` to `Delta t` for a small value of `Delta t`?
    3. Can you use such an average slope to estimate the rate of change at `t=0`? Why or why not?
    4. What is the average slope of the graph from `0` to `Delta t` for a small value of `Delta t`? From `-Delta t` to `0`?
    5. What do you conclude about instantaneous rate of change at `t=0`?
13. Adapt your computer algebra tool or use the zooming feature on your calculator to zoom in on the graph of `ftext[(]t text[)]=|t|^(3//2)` in the vicinity of `text[(]0,0text[)]`.
    1. Is this function locally linear at that point? Why or why not?
    2. What is the average slope of the graph from `-Delta t` to `Delta t` for a small value of `Delta t`?
    3. Can you use such an average slope to estimate the rate of change at `t=0`? Why or why not?
    4. What is the average slope of the graph from `0` to `Delta t` for a small value of `Delta t`? From `-Delta t` to `0`?
    5. What do you conclude about instantaneous rate of change at `t=0`?
14. Adapt your computer algebra tool or use the zooming feature on your calculator to zoom in on the graph of `ftext[(]t text[)]=|t|^(2//3)` in the vicinity of `text[(]0,0text[)]`.
    1. Is this function locally linear at that point? Why or why not?
    2. What is the average slope of the graph from `-Delta t` to `Delta t` for a small value of `Delta t`?
    3. Can you use such an average slope to estimate the rate of change at `t=0`? Why or why not?
    4. What is the average slope of the graph from `0` to `Delta t` for a small value of `Delta t`? From `-Delta t` to `0`?
    5. What do you conclude about instantaneous rate of change at `t=0`?