Chapter 3
Initial Value Problems
3.1 Differential Equations and Initial Values
 Imagine yourself a script writer for your favorite TV detective. Here's the scene: On Monday morning, a wealthy industrialist is found murdered in his office in the climate-controlled building he owns (sorry, owned). The detective has a range of suspects: members of the janitorial crew, the industrialist's ex-wife, his nephew, and the firm's vice-president. Solving the case may depend critically on accurate determination of the time of the crime, as that may show that some (perhaps all but one?) of the suspects could not have been present. How can our detective determine the victim's time of death - and thereby narrow down this list of suspects?
Imagine yourself a script writer for your favorite TV detective. Here's the scene: On Monday morning, a wealthy industrialist is found murdered in his office in the climate-controlled building he owns (sorry, owned). The detective has a range of suspects: members of the janitorial crew, the industrialist's ex-wife, his nephew, and the firm's vice-president. Solving the case may depend critically on accurate determination of the time of the crime, as that may show that some (perhaps all but one?) of the suspects could not have been present. How can our detective determine the victim's time of death - and thereby narrow down this list of suspects?
We will soon put calculus to work to help our detective sort out the suspects. First, we review and formalize the concepts, terminology, and notation introduced in Chapter 2.
We often identify functions by the differential equations they satisfy, so it is important to know what is meant by a function satisfying a differential equation.
| Definition Suppose `y` is a function of `t`, say, . We say the function satisfies an equation in `t` and `y` if can be substituted for `y` in the equation to produce an identity for all time values `t` in some interval. A solution of a differential equation is a function that satisfies the equation. |
Show that the function satisfies the equation
Solution We substitute for `y` in the equation and simplify to see if the equation has become an identity. The largest interval of values for `t` for which this calculation makes sense is . We find
This shows that ![]() equation.
equation.
Show that the function is a solution of the differential equation
Solution Note that we are being asked to show - in possibly unfamiliar words - that a linear function of the form has slope `m`, something we already know. Substitution of in the left side of the equation means calculate its derivative:
Thus, this substitution leads to the identity
(for all values of `t`), so the ![]() linear function does indeed satisfy the differential equation.
linear function does indeed satisfy the differential equation.
Here are two similar-looking differential equations:
and
The slope fields that represent these two equations are shown in Figures 1 and 2 not necessarily in the same order. Match each slope field with the corresponding differential equation. Explain how you decided which is which.
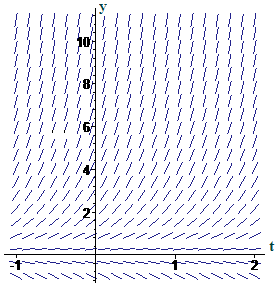 |
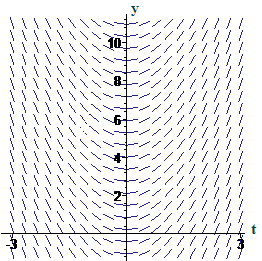 |
| Figure 1 A slope field | Figure 2 Another slope field |
-
Our first differential equation from Activity 1,
,states a problem: Find a function - perhaps many functions - having the property that the derivative is twice as large as the function itself. Give formulas for three different functions that have this property.
-



Use a computer algebra tool to graph your three solutions on a direction field for the differential equation
. How many such functions do you think there are? That is, how many solutions do you think the differential equation has?
Give formulas for three different solutions of our second differential equation from Activity 1,
.-



Use a computer algebra tool to plot the graphs of your three solutions on the slope field for this diferential equation.
How many solutions do you think this differential equation has?
How do the two differential equations (here and in Activity 2) differ from each other? How do their solutions differ?



