Section 3-1-3

Chapter 3
Initial Value Problems

3.1 Differential Equations and Initial Values

3.1.3 Initial Value Problems

For problems in which the independent variable is time `t`, it is often convenient to specify the initial value at $t = 0$ , but that is not required — as you just saw in Activity 4.

We have seen several times now that an initial value problem has a unique solution. This is true for most differential equations — in particular, it is true for all the differential equations we consider in this course. For reference, we record this as a statement we assume to be true.

Fundamental Assumption In this text, we assume that every initial value problem has a unique solution.

If we are looking for a formula for the solution of an initial value problem, our approach will be to

describe all solutions of the differential equation and
determine the unique one that satisfies the initial condition.

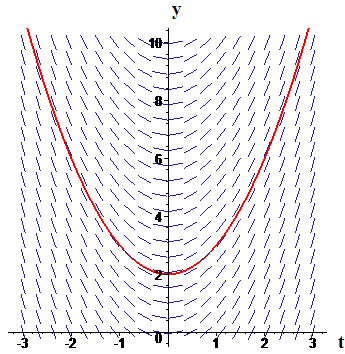
Example 3

Solve the initial value problem

\frac{d y}{d t} = 2 y with y (1) = 3

.

Solution We know from Activity 2 that the solutions of the differential equation are functions of the form

y (t) = C e^{2 t}

We want to select the constant `C` so that

y (1) = 3

.

This means that we must have

3 = y (1) = C e^{2 \times 1} = C e^{2}

or

C = 3 e^{- 2} \approx 0.40601

.

Therefore

y (t) \approx 0.40601 e^{2 t}

.

In Figure 3 we show the slope field for the differential equation

\frac{d y}{d t} = 2 y

and the particular solution for which $y (1) = 3$ .

Figure 3 Slope field and solution for

\frac{d y}{d t} = 2 y, y (1) = 3

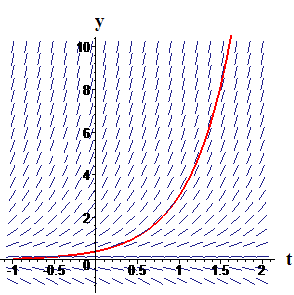
Example 4

Solve the initial value problem

\frac{d y}{d t} = 2 t with y (1) = 3

.

Solution We know from Activity 3 that the solutions of the differential equation are functions of the form

y (t) = t^{2} + C

.

In order to satisfy the condition

y (1) = 3

,

we must have

3 = 1 + C

.

So,

C = 2

.

Thus, the solution of the initial value problem is the function

y (t) = t^{2} + 2

.

In Figure 4 we show the slope field for the differential equation $\frac{d y}{d t} = 2 t$ and the particular solution for which $y (1) = 3$ .

Figure 4 Slope field and solution for

\frac{d y}{d t} = 2 t, y (1) = 3

Go to Back One Page

Go Forward One Page

Contents for Chapter 3