Problems

1. Find three solutions of each of the following differential equations.

   `(dy)/(dt)=7y` `(dy)/(dt)=7t`

   `(dy)/(dt)=1.07y` `(dy)/(dt)=1.07t`

2. For each of the following differential equations, sketch the graphs of three solutions. (You may use your computer, your graphing calculator, and/or your solutions to Problem 1.)

   `(dy)/(dt)=7y` `(dy)/(dt)=7t`

   `(dy)/(dt)=1.07y` `(dy)/(dt)=1.07t`

3. Find the solution of each of the following initial value problems.

   `(dy)/(dt)=7y` with `y=2` at `t=0` `(dy)/(dt)=7t` with `y=2` at `t=0` `(dy)/(dt)=1.07y` with `y=2.3` at `t=0` `(dy)/(dt)=1.07t` with `y=2.3` at `t=0`

4. For each of the following initial value problems, sketch the graph of the solution. (You may use your computer, your graphing calculator, and/or your solutions to Problem 3.)

   `(dy)/(dt)=7y` with `y=2` at `t=0` `(dy)/(dt)=7t` with `y=2` at `t=0` `(dy)/(dt)=1.07y` with `y=2.3` at `t=0` `(dy)/(dt)=1.07t` with `y=2.3` at `t=0`

5. In each of a-d, we show a slope field. By clicking on each image, you can get a page from which you can print your own copy. On each slope field, sketch three solution functions.

   a.	b.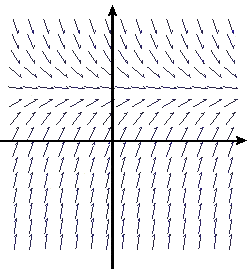
   c.	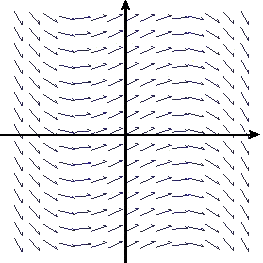d.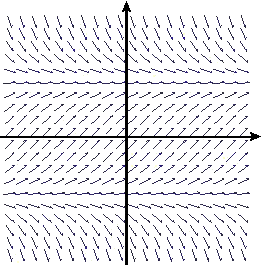

6. 1. Sketch a slope field for `dy text[/] dt=0.5t`. (You can do this on a sheet of notebook paper — precise measurement is not required.)
   2. Sketch a solution.
   3. What feature of the slope field corresponds to the fact that `y` does not appear in the derivative?
7. The slope field in Problem 5c comes from a differential equation of the form `dy text[/] dt=gtext[(]t text[)]`. What geometric characteristic of the field signals the fact that the right-hand side of the differential equation does not depend on `y`?
8. The slope fields in Problems 5b and 5d come from differential equations of the form `dy text[/] dt=g text[(]y text[)]`. What geometric characteristic of these field signals the fact that the right-hand side of each differential equation does not depend on `t`?
9. 1. Let `y=2-2e^(-3t)`. Find `(dy)/(dt)`.
   2. Show that `y=2-2e^(-3t)` is a solution of `(dy)/(dt)=6-3y`.
10. For the slope field in Exercise 12a (repeated here), does the right-hand side of the differential equation depend on `y` only, on `t` only, on both `y` and `t`, or on neither `y` nor `t`? Explain.



11. Table E1 shows the number of disintegrations per minute counted by a Geiger counter that is testing a sample of radioactive barium-137. The disintegration rate of a radioactive substance is proportional to the amount of the substance not yet disintegrated.

    1. Find a formula for a function that approximately fits the data.
    2. Find the half-life of barium-137, that is, the time it takes for a given sample to decay to half the original amount.

    Table E1   Disintegrations per minute
    for radioactive barium-137

    Time (minutes)	Counts per minute
    0	10,034
    1	8105
    2	5832
    3	4553
    4	3339
    5	2648
    6	2035

    
    This problem is adapted from the Core-Plus Mathematics Project.