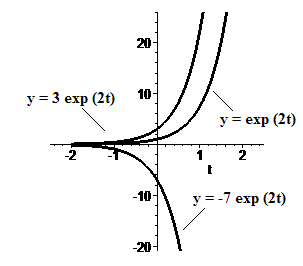
Figure A1 Three solutions of dy/dt = 2y
We saw such functions in the last chapter, for example, `ftext[(]t text[)]=e^(2t)`, `gtext[(]t text[)] = 3 e^(2t)`, `htext[(]t text[)]=-7e^(2t)`. The graphs of these functions are shown in Figure A1.
In general, if `y` is a function of the form `ftext[(]t text[)]=Ce^(2t)`, where C is any constant, then
`f'text[(]t text[)]=d/(dt)Ce^(2t)=C d/(dt)e^(2t)=C*2e^(2t)=2Ce^(2t)=2ftext[(]t text[)]`.
Thus if we substitute `f text[(]t text[)]` for `y` and `f' text[(]t text[)]` for `dy text[/] dt`, we see that `f` satisfies the differential equation `dy text[/] dt=2y`. Since there are infinitely many different choices for `C`, there are infinitely many different solutions of the differential equation.