Chapter 3
Initial Value Problems
3.2 An Initial Value Problem: A Cooling Body
3.2.4 Determining the Proportionality Constant
and Interpreting the Result
Recall that we don't actually know a value for `k` yet. Next we will see how our detective might determine a value of `k` that fits the problem being solved.
Activity 3
Suppose our detective makes a second measurement of body temperature at 9:50 A.M. and finds that the temperature has dropped to 28°C, that is, at . How can we use that information to find `k`? What is `k`?
The numerical value comes from a pocket calculator, which any modern detective always has at hand. Figure 3 shows the slope field for , now drawn with the known value of `k` along with the now fully-known solution through .
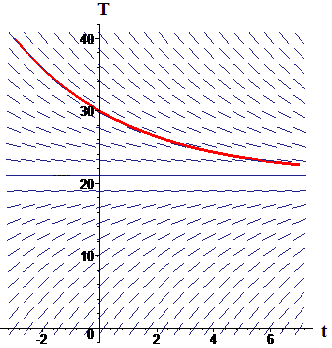 |
| Figure 3 Slope field and solution for |
We are now ready to use the solution of the initial value problem to estimate the time of death.
Activity 4
Use the solution function just obtained to determine the time of death. Once you know the time of death, make a conjecture about the likely murderer.



