Problems

1. Find three solutions of each of the following differential equations.

   `(dy)/(dt)=-7y` `(dy)/(dt)=-7t`

   `(dy)/(dt)=-1.07y` `(dy)/(dt)=-1.07t`

2. For each of the following differential equations, sketch the graphs of three solutions. (You may use your computer, your graphing calculator, and/or your solutions to Problem 1.)

   `(dy)/(dt)=-7y` `(dy)/(dt)=-7t`

   `(dy)/(dt)=-1.07y` `(dy)/(dt)=-1.07t`

3. Find the solution of each of the following initial value problems.

   `(dy)/(dt)=-7y` with `y=20` at `t=0` `(dy)/(dt)=-7t` with `y=20` at `t=0` `(dy)/(dt)=-1.07y` with `y=2.3` at `t=0` `(dy)/(dt)=-1.07t` with `y=2.3` at `t=0` `(dy)/(dt)=-7(y-10)` with `y=20` at `t=0` `(dy)/(dt)=-7(t-10)` with `y=20` at `t=0` `(dy)/(dt)=-1.07(y-10)` with `y=2.3` at `t=0` `(dy)/(dt)=-1.07(t-10)` with `y=2.3` at `t=0`

4. For each of the following initial value problems, sketch the graph of the solution. (You may use your computer, your graphing calculator, and/or your solutions to Problem 3.)
   

   `(dy)/(dt)=-7y` with `y=20` at `t=0` `(dy)/(dt)=-7t` with `y=20` at `t=0` `(dy)/(dt)=-1.07y` with `y=2.3` at `t=0` `(dy)/(dt)=-1.07t` with `y=2.3` at `t=0` `(dy)/(dt)=-7(y-10)` with `y=20` at `t=0` `(dy)/(dt)=-7(t-10)` with `y=20` at `t=0` `(dy)/(dt)=-1.07(y-10)` with `y=2.3` at `t=0` `(dy)/(dt)=-1.07(t-10)` with `y=2.3` at `t=0`

5. In the solution of the cooling body problem, we found that `k` is `ln 9 - ln 7`.
   1. Show that `-k=ln(7/9)`.
   2. Show that the solution function also can be expressed as

   `T=21+9(7/9)^t`.

   3. Recall where the numbers in this expression came from: `21` is the room temperature, `9` is the difference between body temperature at `t=0` and room temperature, and `7` is the difference between body temperature at `t=1` and room temperature. Interpret what this new formula for `T` says about change in the first hour.
   4. Interpret the new formula for `T` as saying that the “same thing” happens in every hour. What same thing?
6. You may think it unnatural to talk about room temperature and body temperature in degrees Celsius. Convert the room temperature, 21°C, and the body temperature at time of death, 37°C, to degrees Fahrenheit. Do these seem like reasonable numbers?

Figure E1   Solution of the
cooling body problem
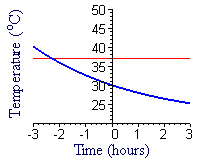
7. 1. In Figure E1 we show a graph of `T=21+9e^(-kt)`, with `k=0.2513144`, along with a graph of normal body temperature, 37°C. Sketch your own graph (or click on the figure to get a printable copy of this one, if you prefer) of the industrialist's body temperature before and after death.
   2. The graph of `T=21+9e^(-kt)` approaches a horizontal asymptote for large values of `t`. Extend your graph from part a to show this asymptote and the approaching graph.
   3. What is the physical meaning of the approach of the temperature graph to this asymptote?
8. In this problem we explore the possible complications created by setting `t=0` at time of death instead of at the time of first temperature measurement. We can still write the differential equation as

   `(dT)/(dt)=-k(T-21)`,

   and we can still transform the equation to

   `(dy)/(dt)=-ky`.

   Thus the solution for `y` still has the form

   `y=y_0e^(rt)`

   where `r=-k`.
   
   
   1. What should `y_0` be in this case?
   2. Suppose we call the time of first measurement `t_1` so that the time of second measurement is `t_1+1`. Suppose the body temperatures at these two times are, as before, 30 and 28°C, respectively. In light of our previous calculation, what do you expect `t_1` to turn out to be? What do you expect `k` to turn out to be?
   3. Use the solution for `y` and the two temperature measurements to write two equations in the two unknown quantities, `k` and `t_1`. Solve these simultaneous equations. Do you get the answers you expected?
9. A company is considering two ways to depreciate a piece of capital equipment that originally cost `\$`14,000 and is worth `\$`10,000 after one year:

   Method I assumes the equipment depreciates at a rate proportional to the difference between its value and its scrap value of `\$`400.

   Method II assumes the equipment depreciates linearly, that is, at a constant rate.

   1. Using method I, find the value of the equipment at the end of 2 years and at the end of 3 years.
   2. Using method II, find the value of the equipment at the end of 2 years and at the end of 3 years.
   3. Which method produces faster depreciation? Explain.
10. Radioactive substances tend to decay at a rate proportional to the amount present at any given time. Let `y_0` be the amount of a radioactive substance present at time `t=0`, and let `y=ytext[(]t text[)]` be the amount present at any time `t`.

    1. Write an initial value problem whose solution is `ytext[(]t text[)]`.
    2. Solve your initial value problem to find a formula for `ytext[(]t text[)]`.
    3. The half-life of a radioactive substance is the time it takes for a given amount to decay to half that amount. Find an expression for half-life that depends only on the proportionality constant in your differential equation.
11. (See Problem 10.) Superman has a violent reaction to green kryptonite, which fortunately has a half-life of only 15 hours as it decays into red kryptonite. It is no longer dangerous to Superman when 90% of the green kryptonite has decayed. If Superman is exposed to pure green kryptonite, for how long is he in danger?
12. (See Problem 10.)
    1. What is the relation between the half-life `H` of a radioactive substance and the “third-life” `T` of the same substance?
    2. What is the relation between the doubling time `D` of a colony of rabbits and the tripling time `T` of the same colony?

Problems 11 and 12 are adapted from Calculus Problems for a New Century, edited by Robert Fraga, MAA Notes Number 28, 1993.