Chapter 3
Initial Value Problems
3.3 Another Initial Value Problem: A Falling Body
3.3.1 Dropping a Marble From the Washington Monument
Suppose we dropped a marble from the window at the top of the Washington Monument. How fast would it be going when it hit the ground, about 535 feet below? Our approach to modeling this problem will involve two initial value problems — one for the velocity of the marble, and another for the distance it travels. However, before we determine the form of these initial value problems, we will estimate the answer we seek by using the tabulated data, repeated from Chapter 2, on approximate position of a falling object for the first 10 seconds of fall.
Time (seconds) |
Distance (meters) |
0.5 |
1.2 |
1.0 |
5.0 |
1.5 |
11.1 |
2.0 |
19.4 |
2.5 |
30.6 |
3.0 |
44.1 |
3.5 |
60.3 |
4.0 |
78.0 |
4.5 |
99.2 |
5.0 |
122.8 |
5.5 |
147.7 |
6.0 |
175.8 |
6.5 |
207.3 |
7.0 |
240.0 |
7.5 |
277.0 |
8.0 |
312.8 |
8.5 |
354.8 |
9.0 |
396.1 |
9.5 |
443.1 |
10.0 |
489.0 |
Table 1 shows simulated positions `s` of a falling object as a function of time `t`. Estimate how fast the marble is falling just before it hits the ground.
As we saw in Activity 1, we can estimate the velocity `v` of the falling object by calculating difference quotients of the data in Table 1. We have , and so on. Thus, the velocity at time is approximately
Similarly
In general,
for each `i` from 0 to 19. In Figure 1 we show the results of these calculations.
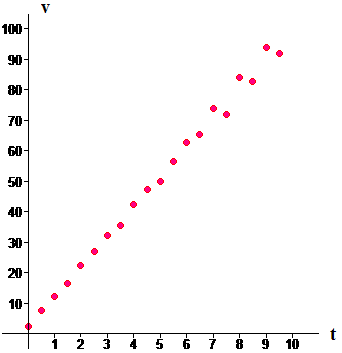 |
| Figure 1 Approximate velocity (in meters per second) of a falling object |
Activity 2
-
In Chapter 2 we showed that position `s` might be a function of the form . Explain why this would imply that velocity `v` is a linear function of `t`.
Explain why, if the velocity is linear, then the acceleration must be constant.
-
What do you see in Figure 1 that tells you that the acceleration (the time derivative or rate of change of `v`) is approximately constant?




