Chapter 3
Initial Value Problems
3.3 Another Initial Value Problem: A Falling Body
3.3.3 An Initial Value Problem for Velocity
Now that we have determined an appropriate differential equation, we'll look for the particular solution to model the fall of the marble.
Find a family of solutions of the differential equation
.Use your graphing tool to check that your solution functions agree with the direction field for the differential equation.
Find the solution of the initial value problem
.Find the solution of the initial value problem
.Give a physical interpretation of this problem and its solution.
Find the solution of the initial value problem
.Give a physical interpretation of this problem and its solution.
For our falling marble (which has zero initial speed), we now know velocity as a function of time. Recall that we asked "How fast would it be going when it hit the ground, about 535 feet below?" The formula would answer this question if we knew how long it takes to fall `535` feet. But that's a question about the functional relationship between distance and time, which we don't know yet. However, we can read as a differential equation relating distance and time - because - and we can set up another initial value problem:
In Figure 3 we show the slope field for this initial value problem.
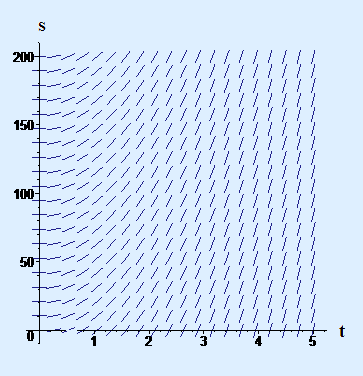
Figure 3 Slope field for position of a falling object
Activity 4
- Find a family of solutions of the differential equation
Find the solution of the initial value problem
Use your graphing tool to sketch this solution on the slope field for the differential equation.


Find the solution of the initial value problem
Use the same tool as in part b to sketch this solution on the slope field for the differential equation.
Now that we have explicit formulas for position and velocity of the falling marble, we can determine the time of fall from the position formula and then the speed at impact from the velocity formula.
Example 1
How long does the marble fall?
Solution The time to fall `535` feet is the (positive) solution of
![]() We find , or seconds.
We find , or seconds.
You can finish the marble problem in Checkpoint 3.
Finally, we illustrate how all the pieces fit together in an extended example that treats a similar, but different, situation.
Example 2
Suppose the marble is thrown upward with a velocity of `10` feet per second from a height of `535` feet. How long will it take to hit the ground? How fast will it be traveling when it reaches the ground?
Solution We have assumed throughout the previous discussion that down is the positive direction, so an upward initial velocity is negative. As we saw in Activity 3, the velocity function is
Now we have a new initial value problem for the distance traveled:
We know that a function has derivative `gt` when it has the form
We also know that a function has the constant derivative `10` when it has the form
Thus, using our rule for the derivative of a difference, we find that any function of the form
(where `K` is a constant) satisfies the differential equation
Our initial condition, , requires that `K` be `0`, so the unique solution of the initial value problem for distance fallen is
We leave it to you to finish the example in the next Checkpoint.




