Chapter 3
Initial Value Problems
3.3 Another Initial Value Problem: A Falling Body
Problems
- Differentiate each of the following functions.
- `ftext[(]t text[)]=e^(3t)`
- `gtext[(]t text[)]=e^(-2t)`
- `Ptext[(]t text[)]=1.2^t`
- `htext[(]t text[)]=3t-5t^2`
- `phitext[(]t text[)]=6-e^(-3t)`
- `gtext[(]t text[)]=2t+e^(-t)`
- `Ftext[(]t text[)]=e^(-3t)+6t^2`
- `Gtext[(]t text[)]=6-e^(-2)`
- `ptext[(]t text[)]=2^(3t)`
- `Htext[(]t text[)]=3+t+5t^2`
- `psitext[(]t text[)]=e^(-3t)-6t+7`
- `rtext[(]t text[)]=2t^3-e^(-t)`
- `Qtext[(]t text[)]=7t^4+5t^3-4t^2+3t-10`
- `wtext[(]t text[)]=t^3+sqrt(2)e^(2t)`
-
Use your graphing tool to graph each of the following functions together with its derivative, using your answer to the corresponding part of Problem 1. In each case note any features of the derivative graph that correspond to what you observe about slopes on the graph of the original function. (This is a way to check your work on Problem 1. If the features of your derivative graph don't match slope features on the original graph, that may mean you did something wrong in your algebraic calculation.)
- `ftext[(]t text[)]=e^(3t)`
- `gtext[(]t text[)]=e^(-2t)`
- `Ptext[(]t text[)]=1.2^t`
- `htext[(]t text[)]=3t-5t^2`
- `phitext[(]t text[)]=6-e^(-3t)`
- `gtext[(]t text[)]=2t+e^(-t)`
- `Ftext[(]t text[)]=e^(-3t)+6t^2`
- `Gtext[(]t text[)]=6-e^(-2)`
- `ptext[(]t text[)]=2^(3t)`
- `Htext[(]t text[)]=3+t+5t^2`
- `psitext[(]t text[)]=e^(-3t)-6t+7`
- `rtext[(]t text[)]=2t^3-e^(-t)`
- `Qtext[(]t text[)]=7t^4+5t^3-4t^2+3t-10`
- `wtext[(]t text[)]=t^3+sqrt(2)e^(2t)`
- Compare the impact speed for the marble dropped from 535 feet (Checkpoint 3) with that for the marble thrown upward from the same point at 10 feet per second (Checkpoint 4). Is this what you would expect? Explain.
- Suppose a marble is thrown downward with a velocity of 10 feet per second from a height of 535 feet. How long will it take to hit the ground? How fast will it be traveling when it reaches the ground?
-
-
Checkpoint 3 and Problem 4 tell us that a marble thrown up at 10 feet per second from 535 feet hits the ground at the same speed as a marble thrown down at 10 feet per second from the same height. Explain this by showing that the marble thrown up is traveling at 10 feet per second when it passes the throwing point on the way down.
-
In Figure E1 we show a portion of the slope field and solution for the position of a marble thrown at 10 feet per second. Was the marble thrown up or down? Explain your answer. Also explain the significance of the positive value of `t` at which the position curve crosses the `t`-axis.
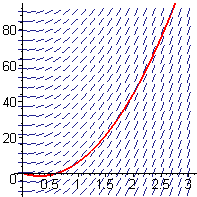 Figure E1 Slope field for
Figure E1 Slope field for
position of a falling object -
-
Suppose we check the answer to Checkpoint 4 by substituting back into the equation
`535=1/2gt^2-10t`.
On the right-hand side we get`1/2*32.17*text[(]6.09text[)]^2-10*6.09=535.66`,
which doesn't even round off to the expected 535. Explain what is going on in terms of what you learned in Chapter 1 about significant digits. -
 Suppose a raindrop falls to the earth from a cloud `3000` feet high, and the only force acting on the raindrop is that of gravity. How long does it take the raindrop to fall? How fast is it going when it strikes the ground? Does this fit with your experience with rain?
Suppose a raindrop falls to the earth from a cloud `3000` feet high, and the only force acting on the raindrop is that of gravity. How long does it take the raindrop to fall? How fast is it going when it strikes the ground? Does this fit with your experience with rain?

