Chapter 4
Differential Calculus and Its Uses
4.1 Derivatives and Graphs
We know that local linearity ties the derivative of a function f to the local slope of the graph of f. We should not be surprised then that derivative calculations can tell us a great deal about the shape of the graph of a function. In this section we explore this connection with particular emphasis on the use of the derivative to identify highest and lowest points on a graph.
4.1.1 Local Maximum and Minimum Values
We begin by examining the relationship between the graph of a function and the values of the derivative.
Activity 1
 A child releases a helium filled balloon on a still day. The balloon rises for a while, and then, because of a slow leak, it descends until it catches in a tree. The graph in Figure 1 plots the vertical velocity of the balloon as a function of time.
A child releases a helium filled balloon on a still day. The balloon rises for a while, and then, because of a slow leak, it descends until it catches in a tree. The graph in Figure 1 plots the vertical velocity of the balloon as a function of time.
-
At what time after release was the balloon at its highest point?
On a piece of scratch paper, sketch an approximate graph of the height as a function of time.
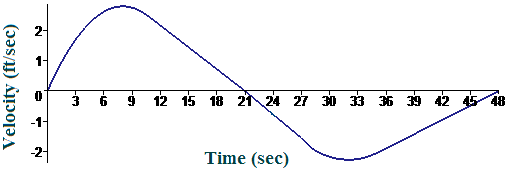 |
| Figure 1 Velocity of the balloon as a function of time |
The correspondence in Activity 1, between maximum values of a function and zeros of the derivative, is one we will exploit often. For the moment, we'll illustrate this by describing how to sketch a graph by hand.
Sketch the graph of the function on the domain by hand. (Suppose someone else is using your computer and the batteries in your calculator have run down.)
Solution We begin by calculating the derivative of `f`:
We can explore the sign of the derivative by examining the signs of the factors — sign changes can occur only where one of the factors changes sign. We see that the derivative is negative at and remains negative until . At that point the derivative switches over to positive values and remains positive until Between and , the derivative is negative again. Then at the derivative becomes positive and remains that way.
Now we use this information to sketch the graph of `f`:
-
At , the function value is . As `t` increases, the graph decreases until it bottoms out at `text[(]0,-1text[/]6text[)]`.
-
Beyond , the graph starts to rise and continues upward until it reaches `text[(]0,1text[/]12text[)]`.
At this point the graph turns downward again and decreases to `text[(]2,-1text[/]6text[)]`.
Here the graph turns upward and continues to rise for all
Figure 2 shows the graph of f, which could be drawn using this information. ![]() Check to see that this sketch reflects each point of the discussion.
Check to see that this sketch reflects each point of the discussion.
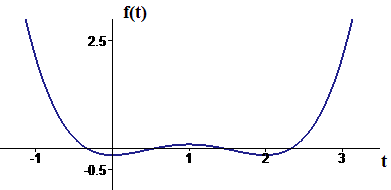 |
| Figure 2 Graph of |
Now compare the graph of f with the graph of in Figure 3. Notice that two of the zeros of ( and ) correspond to minimum values of f. The derivative must be zero at points where the graph stops increasing and starts decreasing — at maximum values — and it also must be zero at points where the graph stops decreasing and starts increasing — at minimum values. Thus, the zeros of the derivative are helpful in locating both minimum and maximum values of the function.
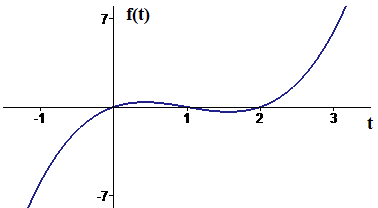 |
| Figure 3 Graph of |
The remaining zero of the derivative at corresponds to a maximum value. However, it is a maximum only relative to values at nearby points. The maximum value over the whole domain occurs at the two end points of the interval, where . At these end points the derivative is not zero. These are maximum values only because we are not considering values of t less than or greater than 3.
| Definitions A function has a local maximum value at if for all `t` close to . The corresponding point on the graph of `f` is called a local maximum point. Similarly, the function has a local minimum value at if for all `t` close to . The corresponding point on the graph of `f` is called a local minimum point. Collectively, local maximum and minimum points are called local extreme points, and local maximum and minimum values are called local extreme values. |
Figure 4 illustrates local extreme points that are not at the end points of a domain. Observe that this function clearly has values that are smaller (more negative) than the local minimum. If the domain continues to the right, it may also have values that are larger than the local maximum.
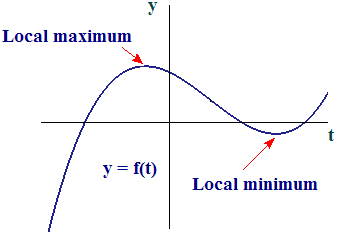 |
| Figure 4 Local extreme points |
Identify the local maxima and minima of on the domain .
Solution Look again at the graph of in Figure 5. The function has local minimum values at and and a local maximum value at , the three values of t at which . The function also has a local maximum value at each of the endpoints of the interval, and . At these points the derivative is not zero. These are local maximum points because and are bigger than any nearby values ![]() of `f` in the domain.
of `f` in the domain.
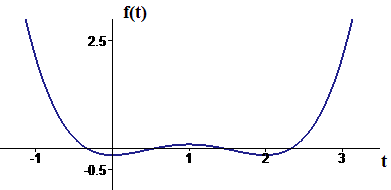 |
| Figure 5 Graph of |
Let's summarize what we have discovered about the relationship between the graph of a function `f` and values of its derivative .
At points where the derivative of the function is positive, the graph of the function is increasing (from left to right).
At points where the graph of the function is increasing, the value of the derivative is positive.
At points where the derivative of the function is negative, the graph of the function is decreasing (from left to right).
At points where the graph of the function is decreasing, the value of the derivative is negative.
These four statements reflect the local linearity of the graph. When we zoom in on a point of the graph, we see a straight line. If the line slopes upward, the graph is increasing and the derivative is positive. If the line slopes downward, the graph is decreasing and the derivative is negative.
At points where the graph of the function changes from increasing to decreasing, the function has a local maximum value and the derivative is zero.
At points where the graph of the function changes from decreasing to increasing, the function has a local minimum value and the derivative is zero
It is important to note what is not included in the last two statements. A zero of the derivative does not mean that the graph must change its vertical direction. For example, consider the graph of the function in Figure 6. The derivative of `f` at is zero, but the graph goes from increasing to increasing. In other words, there is neither a local maximum nor a local minimum value for `f` at — even if we restrict our attention to just the vicinity of .
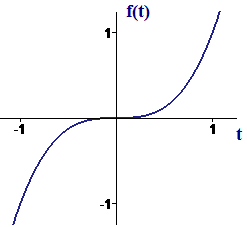 |
| Figure 6 Graph of |
Image credit




