Section 4-1-2

Chapter 4
Differential Calculus and Its Uses

4.1 Derivatives and Graphs

4.1.2 Global Maximum and Minimum Values

Now we concentrate on finding largest and smallest values of a function over a specified domain for the independent variable. This is the form in which differential calculus is usually applied to optimization problems. The local information provided by the derivative identifies candidates for the best or worst function values, and the end points (if any) identify additional candidates. Once we have a finite list of candidates, it is easy to check the value at each and choose the largest or smallest.

Example 3

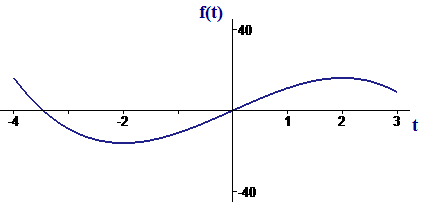
Find the largest and smallest values of $f (t) = - t^{3} + 12 t$ on the interval $- 4 \leq t \leq 3.$

Solution We display the graph of f in Figure 7. (Check the graph with your graphing tool.) It is clear from the graph that the smallest value occurs at one of the points where the derivative is zero, i.e., at a root of the equation $- 3 t^{2} + 12 t = 0$ . These roots are $t = \pm 2$ . The smallest value of f is clearly the local minimum that occurs at $t = - 2$ : $f (- 2) = - 16$ . Note that the function also has a local minimum at $t = 3$ , but $f (3)$ is clearly not the smallest (or largest) value of f.

Figure 7 Graph of

f (t) = - t^{3} + 12 t

On the other hand, it is not clear from the graph whether the largest value occurs at $t = 2$ (the other zero of the derivative) or at $t = - 4$ (the left-hand endpoint of the interval). In fact, $f (2)$ and $f (- 4)$ are both equal to 16, which is the largest value of `f` on the given domain.

The largest and smallest values of a function and the corresponding points on the graph also get special names.

Definitions If

f (t_{0})

is greater than or equal to

f (t)

for all values of t in the domain, then f has a global maximum value at

t = t_{0}

. Similarly, if

f (t_{0})

is less than or equal to

f (t)

for all values of t in the domain, then f has a global minimum value at

t = t_{0}

. The corresponding points on the graph of f are called global maximum points and global minimum points, respectively. Collectively, global maximum and minimum points are called global extreme points, and global maximum and minimum values are called global extreme values.

We summarize what we have learned about the location of global extreme values of a function.

A global extreme value (maximum or minimum) may occur at a point where the derivative is zero.
A global extreme value (maximum or minimum) may occur at one of the boundary points of the domain.

Checkpoint 2

Contents for Chapter 4

Chapter 4 Differential Calculus and Its Uses

4.1 Derivatives and Graphs

Chapter 4
Differential Calculus and Its Uses