Chapter 4
Differential Calculus and Its Uses
4.1 Derivatives and Graphs
4.1.3 Minimizing Production Cost
 The Orlando Juice Company sells its product in distinctive rectangular paper boxes. They would like to make the boxes as inexpensively as possible, without violating various design specifications. In particular, the boxes must be stronger on the top and bottom than on the sides, so it costs more to make the top and bottom.
The Orlando Juice Company sells its product in distinctive rectangular paper boxes. They would like to make the boxes as inexpensively as possible, without violating various design specifications. In particular, the boxes must be stronger on the top and bottom than on the sides, so it costs more to make the top and bottom.
The one gallon container for O.J. is to be a box with a square top and bottom. If the top and bottom cost `2.5` times as much as the sides, what dimensions should the box have to minimize the cost of production?
We'll approach this problem by finding a formula for the cost of manufacturing a box of a given shape and then decide what shape has the lowest cost.
 |
| Figure 8 Orange juice box |
Suppose that both the square top and square bottom are `s` inches on a side and the height is `h` inches. (See Figure 8.) Then each of the four sides has surface area `sh` square inches, and each of the top and bottom has surface area square inches. If `c` is the cost per square inch of the sides, then the total cost is
We can express the cost in terms of `s` alone by eliminating `h`. The volume of the box — one gallon — is 231 cubic inches. This volume is also , so , and . Thus the cost of manufacturing the box is
Now we want the value of `s` that minimizes `C`.
The value of `c` plays no role in the minimization calculation — just in what that minimum cost is. So, we can concentrate on minimizing the weighted surface area function,
A graph of this function is shown in Figure 9.
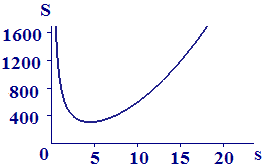 |
| Figure 9 Weighted surface area S versus side length s |
It is apparent that both large values of `s` (thin wide boxes) and small values of `s` (tall narrow boxes) yield large surface areas — and therefore large production costs. The minimum surface area seems to correspond to a value of `s` around `5` inches.
We could zoom in to try to obtain a better estimate of the optimal `s`, but the graph is very flat at this point. (Try it on your graphing tool.) Another approach is to calculate the derivative of the surface area function and find where this derivative is zero. The graph of is plotted in Figure 10. Notice that this graph shows us that the optimal value of s is not 5.
 |
| Figure 10 The graph of |
Here is the start of the derivative calculation:
To complete this calculation, we need a formula for the derivative of the reciprocal function:
Image credit


