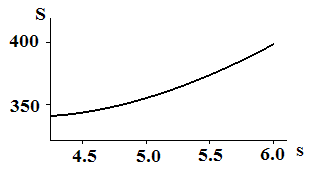
Figure A5 Graph of S versus s for r = 3.4
The formula for the total cost of a juice box with the top and bottom `r` times as expensive per unit area as the sides is
`C=4((231c)/s)+2(rcs^2)=c(924/s+2rs^2)`.
As before, it is enough to minimize the formula for the weighted surface area, `S=924text[/]s+2rs^2`. The optimal s satisfies `dS text[/] ds=0`. Since `dS text[/] ds=-924text[/]s^2+4rs`, the value of s that we want satisfies `-924text[/]s^2+4rs=0`. Solving this equation, we find `s^3=231text[/]r` or
`s=(231/r)^(1/3)`.
Now, if we assume that `r` increases to `3.4`, this formula gives `s=4.08`. But this is outside the Sales Department's restrictions. It follows that there is no value of `s` in the interval `[4.25,6]` where `dS text[/] ds=0`. Thus the minimum value of `s` must occur at one or the other end point. Indeed, it occurs at `s=4.25`. Figure A5 shows the graph of `S` versus `s` over this interval.
