4.2.3 Terminology: Zeros, Critical Values,
         and Inflection Points

We have seen that we get a lot of information about the graph of a function `f` by finding the values of `t` at which $f\left(t\right)$ or $f\prime \left(t\right)$ or $f\prime \prime \left(t\right)$ is zero. We summarize here the common terminology associated with these special values of `t`.

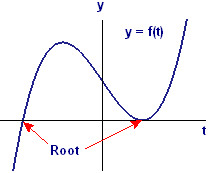Figure 1   Crossing and touching the horizontal axis

We have already seen that the zeros of a function tell us where the function might change from positive to negative values or vice versa. More specifically, they tell us where the graph either crosses or touches the horizontal axis. (See Figure 1.)

Also we have seen that the zeros of $f\prime$ [roots of $f\prime =0$] tell us where the graph of `f` might change from increasing to decreasing or vice versa. More specifically, they tell us where the graph of `f` might have a local maximum or a local minimum.

Now the zeros of $f\prime \prime$ [roots of $f\prime \prime \left(t\right)=0$] tell us where the graph of `f` might change from concave down to concave up or vice versa. The points on the graph where a change of concavity occurs are given a special name.

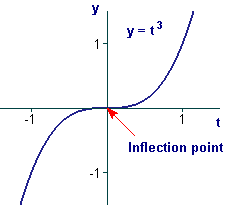Figure 2   An inflection point

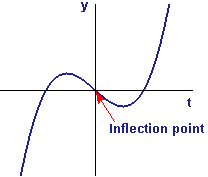Figure 3   An inflection point that is not a critical value

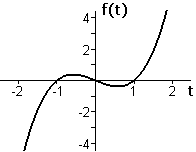Figure 4   $f\left(t\right)=t^3-t$

The origin is both a critical point and an inflection point of the graph of $y=t^3$ (Figure 2). In particular, this is an example of a critical point that is neither a maximum nor a minimum point.

The origin is also an inflection point of the graph in Figure 3. In this case, there are two critical points, neither of them at the origin. (Where are they?)

Example 2

Find the zeros, critical points, and inflection points for the function `f` defined by $f\left(t\right)=t^3-t\mathrm{.}$ Determine what each tells us about the graph of `f`.

Solution   The zeros are the roots of

${\displaystyle t^3-t=0.}$

Since $t^3-t=t(t-1)(t+1),$ the zeros are `0`, `1` and `-1`. (See Figure 4.) These are the numbers at which $f\left(t\right)$ changes sign, from negative to positive at `-1`, from positive to negative at `0`, and from negative to positive at `1`.

The critical values of `f` are the zeros of $f\prime$, i.e., the roots of $3t^2-1=0$:

As we can see from the graph, `f` has a local maximum value at $t=-1/\sqrt{3}$ and a local minimum value at $t=1/\sqrt{3}$. We can confirm this with the second derivative:

and

The second derivative of `f` has a zero when $6t=0,$ that is, when $t=0.$ The corresponding point $(0,0)$ on the graph is an inflection point, since the second derivative changes from negative to positive at this point. Equivalently, the graph changes from concave downward to concave upward at this point.