Exercises

1. For each of the following functions:
   1. Calculate the second derivative,
   2. Identify the range of values of `t` for which the graph is concave up and the range of values for which the graph is concave down.
   
   

   `ftext[(]t text[)]=e^(4t)` `gtext[(]t text[)]=e^(-3t)` `htext[(]t text[)]=3^t-t^3`

   `utext[(]t text[)]=t+1` `vtext[(]t text[)]=t^3+t^2+t+1` `wtext[(]t text[)]=t^2+t+1`

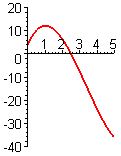
2. Figure E1 shows a graph of the polynomial function `ftext[(]t text[)]=t^4-18t^2-10t+39`.
   1. Approximately where is `ftext[(]t text[)]=0`?
   2. Approximately where is `f'text[(]t text[)]=0`? Click on the graph to get a printable copy, and mark these points on your copy.
   3. On what intervals is `f'` positive?
   4. On what intervals is `f'` negative?

Figure E1  Graph of f(t) = t⁴ - 18t² - 10t + 39
3. 1. For the function graphed in Figure E1, approximately where is `f''text[(]t text[)]=0`?
   2. On what intervals is `f''text[(]t text[)]` positive?
   3. On what intervals is `f''text[(]t text[)]` negative?
4. 1. Find the zeros of the function `f` defined by the formula `ftext[(]t text[)]=t^3-36t`.
   2. Calculate `f'`, and find the zeros of `f'`.
   3. Calculate `f''`,and find the value of `f''` at each zero of `f'`.
   4. For each zero of `f'`, decide whether the corresponding point on the graph is a local maximum, a local minimum, or neither.
   5. Decide whether the zero of `f''` represents an inflection point.
5. The graphs of three functions appear in Figure E2. Identify which is the graph of `f`, which is the graph of `f'`, and which is the graph of `f''`.

   

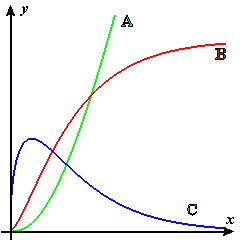
   Figure E2  Identify the function f and its first two derivatives

6. Figure E3 shows the graph of the derivative `f'text[(]x text[)]` of an unknown function `ftext[(]x text[)]`.
   1. From the figures A–F following, choose the one that shows the graph of `ftext[(]x text[)]`.
   2. From the figures A–F following, choose the one that shows the graph of `f''text[(]x text[)]`.

   
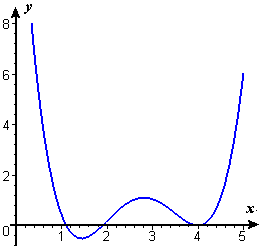
   Figure E3  Graph of f '(x)

   A.	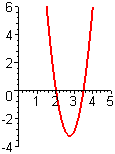B.	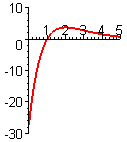C.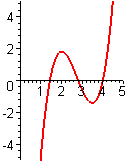
   D.	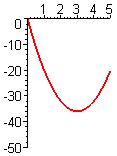E.	F.