Problems

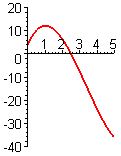
1. Figure P1 shows a graph of the polynomial function `ftext[(]t text[)]=t^4-18t^2-10t+39`.
   1. Approximately where is `ftext[(]t text[)]=0`?
   2. Approximately where is `f'text[(]t text[)]=0`? Click on the graph to get a printable copy, and mark these points on your copy.
   3. On what intervals is `f'` positive?
   4. On what intervals is `f'` negative?
   5. Sketch a graph of `f'`.
   6. Confirm your results in parts (b) through (e) by calculating `f'` and graphing it with your graphing tool.

Figure P1  Graph of f(t) = t⁴ - 18t² - 10t + 39
2. 1. For the function graphed in Figure P1, approximately where is `f''text[(]t text[)]=0`?
   2. On your printed copy of the graph, mark the points where `f''text[(]t text[)]=0`.
   3. On what intervals is `f''text[(]t text[)]` positive?
   4. On what intervals is `f''text[(]t text[)]` negative?
   5. Sketch a graph of `f''text[(]t text[)]`.
   6. Confirm your results in parts (a) through (e) by calculating `f''` and graphing it with your graphing tool.
3. 1. Find the zeros of the function `f` defined by the formula `ftext[(]t text[)]=t^3-36t`.
   2. Calculate `f'`, and find the zeros of `f'`.
   3. Calculate `f''`,and find the value of `f''` at each zero of `f'`.
   4. For each zero of `f'`, decide whether the corresponding point on the graph is a local maximum, a local minimum, or neither.
   5. Decide whether the zero of `f''` represents an inflection point.
   6. Sketch a graph of `f`. After making your own graph, you can check your work with your graphing tool.
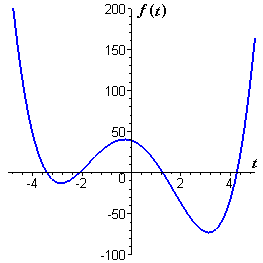
4. The graphs of three functions appear in Figure P2. Identify which is the graph of `f`, which is the graph of `f'`, and which is the graph of `f''`. Explain your conclusions.

   

   Figure P2  Identify the function f and its first two derivatives

5. Imagine the graph of a polynomial of degree 3 or higher. Imagine that this graph is a map of a relatively flat road. Imagine that you are riding a bicycle along this road in the positive `x`-direction.
   1. Describe what you experience as you pass through a point at which the second derivative of the polynomial is zero.
   2. What are you doing along a stretch of the road on which the second derivative is positive?
   3. What are you doing along a stretch of the road on which the second derivative is negative?
6. Sketch the graph of a function that is
   1. increasing at an increasing rate.
   2. increasing at a decreasing rate.
   3. decreasing at an increasing rate.
   4. decreasing at a decreasing rate.
7. Figure P3 shows the graph of the derivative `f'text[(]x text[)]` of an unknown function `ftext[(]x text[)]`.
   1. From the figures A–F following, choose the one that shows the graph of `ftext[(]x text[)]`.
   2. From the figures A–F following, choose the one that shows the graph of `f''text[(]x text[)]`.
   3. Justify each of your choices in parts (a) and (b).

   
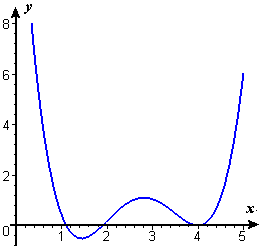
   Figure P3  Graph of f '(x)

   A.	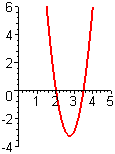B.	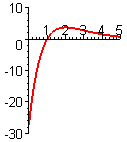C.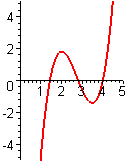
   D.	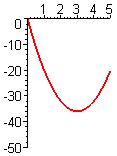E.	F.