Chapter 4
Differential Calculus and Its Uses
4.3 Solving Nonlinear Equations
by Linearization: Newton's Method
4.3.2 Newton's Method
Here's our plan for finding a root r of the equation We start close to say, at We find the slope of the graph at the point as Our next guess will be the number at which a line of slope crosses the horizontal axis. That number won't necessarily be the solution of that we seek, but it will usually be much closer than was. Then we start over, replacing by . The key to the success of this idea is the "much closer" that we achieve at each step, which usually makes it unnecessary to do more than a few steps.
In our example, so We start at the point , so our slope (see Figure 3) is
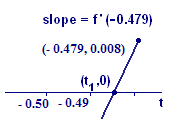 |
| Figure 3 First approximation step |
Now our calculation proceeds very much as before. Again we equate two expressions for the slope: the value, `1.670918828`, of the derivative and the slope of the line from the upper right point to the point of intersection with the `t`-axis. Equating these two slope calculations, we find
When we clear the fraction and solve for we get
This is a little better than before — the error is about `0.00012` — but it's still not correct to `10` places. On the other hand, if we start again from and calculate the next guess , we get
Now we're getting somewhere. The error, when we compare this answer with that from a calculator's or computer's Root function, is about so we're already at `9`-place accuracy, with just two steps.
Let's outline the calculation in general. The slope of the graph of `f` at is The point is also on the line through with the same slope. Thus, the slope also has the form "rise over run" or
where represents . Now we set our two expressions for slope equal:
And we solve for :
This equation tells us how to get from to : Subtract the ratio of the function value at to the slope at . Look at Figure 4, and explain the calculation to yourself in these terms: The run is the rise divided by the slope. Be sure you understand where the minus sign comes from.
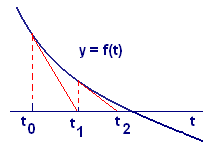 |
| Figure 4 First two steps in Newton's Method for solving |
Now we get from in exactly the same way. Then from , and so on. In fact, what we have here is an iterative formula for generating the numbers , , , ... from the starting point :
This formula is generally known as Newton's Method for solving equations.

