Chapter 4
Differential Calculus and Its Uses
4.3 Solving Nonlinear Equations
by Linearization: Newton's Method
4.3.3 Examples of Newton's Method
Find a root of the equation
 |
| Figure 5 Graph of |
Solution We start by setting A graph of this function (Figure 5) shows that there is a solution a little bigger than `0.5`. Suppose we begin with a guess that is not very close, say, Then
Now for all `t`, so
Then
The next two steps, calculated in the same way, give
and
Since it is likely that all six decimal places shown for are correct. Indeed, since the slope near the root is about `-2`, the difference between and the exact root (a run) should be about half the difference between and zero (the corresponding rise). Run equals rise ![]() over slope.
over slope.
Our next example illustrates a lengthier calculation with Newton's Method. We will solve an equation without first zooming in to find a good starting guess.
Example 2
Find the smallest (left-most) solution of without zooming in.
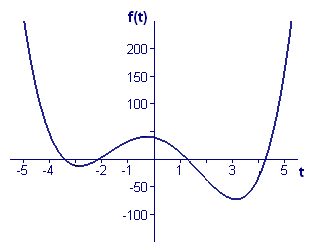 |
| Figure 6 Graph of |
Solution From the graph in Figure 6 we see that the solution is between `-4` and `-3`. We could use either `-4` or `-3` as a starting point — let's use `-4.` We have
Table 1 shows our calculations. Check the calculation of with your own calculator or computer algebra system.
| `n` | ||||
| 0 | -4.0 | 47.0 | -122.0 | -0.385246 |
| 1 | -3.614754 | 10.683527 | -68.796815 | -0.155291 |
| 2 | -3.459463 | 1.402967 | -51.069143 | -0.027472 |
| 3 | -3.431991 | 0.040318 | -48.144002 | -0.000837 |
| 4 | -3.431154 | 0.000058 | -48.055859 | -0.000001 |
| 5 | -3.431153 | 0.000058 | -48.055859 | -0.0000002 |
This is as far as we can go with six decimal place accuracy. The change in `t` in the last column is too small to affect the sixth place, which is why neither `f` nor `f'` changed in the last step. We can safely conclude that the solution we seek is `t=-3.43115` to five-place accuracy (6SD). The next digit remains in doubt because of our rounding.
Notice how rapidly the changes in the last column got small. That only hints at how effective Newton's method can be — a matter you may take up in a ![]() project related to this chapter.
project related to this chapter.


