Problems

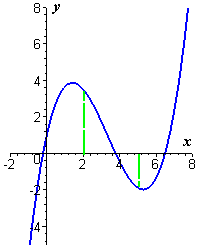
1. 1. Use Newton's Method to find all the zeros of the function in Example 2:

   `ftext[(]t text[)]=t^4-18t^2-10t+39`.

   2. Check your answers by calculating the value of `ftext[(]t text[)]` at each zero.
   3. Check your answers by zooming in on the graph.
   4. Check your answers by using the Solve or Root function of your graphing tool.
2. 1. Use Newton's Method to find all three solutions of the equation `3x^2=e^x`.
   2. Check your answers by substituting into the original equation.
   3. Check your answers by zooming in on a relevant graph.
   4. Check your answers by using the Solve or Root function of your graphing tool.
3. 1. Use Newton's Method to find the root of `t^2-e^(-3t)=0`.
   2. Check your answers by substituting into the original equation.
   3. Check your answers by zooming in on a relevant graph.
   4. Check your answers by using the Solve or Root function of your graphing tool.
4. Let `ftext[(]t text[)]=t^3+8t^2+t-6`.
   1. Calculate the values of `f` at `t=-10`, `t=-5`, `t=0`, and `t=2`.
   2. Why do your calculations in part (a) show that `f` has at least three zeros?
   3. How do you know that `f` does not have more than three zeros?
   4. Use Newton's Method to find all zeros of `f`.
   5. Check your answers. (Refer to Problems 1-3 for some ways to check.)
5. Let `ftext[(]t text[)]=e^t+e^(-t)-2t^2.
   1. Find the four zeros of `f`.
   2. Find the three zeros of `f'`.
   3. Find the smallest value of `f` and the two values of `t` where `f` has its smallest value.
   4. Find the largest value of `f` between `t=-1` and `t=1`.
   5. Use the information from parts (a) through (d) to sketch the graph of `f`. Use your graphing tool to check your work.
6. Use Newton's Method to find (approximately) all solutions of each of the following equations. Check your answers by using the Solve or Root function on your calculator or computer.

   a.   `x^3+5x=10`	b.   `x^3+5x=e^x`	c.   `x^3+5x=-e^x`
   d.   `x^3-5x=10`	e.   `x^3-5x=e^x`	f.   `x^3-5x=-e^x`

7. Let `ftext[(]t text[)]=t^4-10t^2+e^(2t)`.
   1. Find all the zeros of `ftext[(]t text[)]`. (There are four.)
   2. Find all the zeros of `f'text[(]t text[)]`. [There are three — how must they be related to the zeros of `ftext[(]t text[)]`?]
   3. Find all the zeros of `f''text[(]t text[)]`. [There are two — how must they be related to the zeros of `f'text[(]t text[)]`?]
   4. Sketch the graphs of `ftext[(]t text[)]`, `f'text[(]t text[)]`, and `f''text[(]t text[)]`. (Use your graphing tool to check.)
   5. Find all local maximum points and all local minimum points of the graph of `f`.
   6. Find all inflection points of the graph of `f`.
8. If Newton's Method is applied to `ftext[(]x text[)]=3x+4`, and `x_0` is `15`, what will `x_17` be?
9. Find at least one solution to the equation `4x^3-x^4=30`, or explain why no such solution exists.

 

Suppose you are using Newton's Method to find a zero of the function `f` whose graph is shown in Figure P1. If your starting point is at `x_0=2`, label where (approximately) `x_2` will be. (Click on the figure to get a larger, printable copy.) Suppose you try again with Newton's Method for the same function `f`. If your starting point is at `x_0=5`, label where (approximately) `x_2` will be. If you knew a formula for this function, do you think its zeros could be found by Newton's Method? Explain your answer.

Figure P1   Start Newton"s Method at 2 and at 5

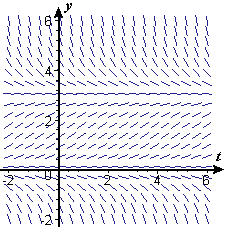
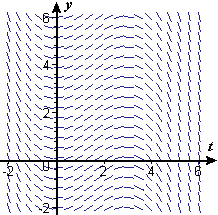
11. Figure P2 shows a slope field for `dy text[/] dt=0.3ytext[(]3-y text[)]` for `t` ranging from `-2` to `6` and `y` also ranging from `-2` to `6`. Figure P3 shows a slope field for `dy text[/] dt=0.3t text[(]3-t text[)]` with both `t` and `y` ranging from `-2` to `6`. Click on either figure to get a printable page that shows both. You can use the printed page for drawing on the slope fields.
    1. On Figure P2 sketch the solution of `dy text[/] dt=0.3ytext[(]3-y text[)]` for which `ytext[(]0text[)]=0.5`.
    2. On Figure P3 sketch the solution of `dy text[/] dt=0.3t text[(]3-t text[)]` for which `ytext[(]0text[)]=0.5`.
    3. Solve the initial value problem: `dy text[/] dt=0.3text[(]3t-t^2 text[)]` with `ytext[(]0text[)]=0.5`.
    4. Your graph in part (b) should show that the solution in part (c) has a root near `t=5`. Take that as a starting guess, and find the next approximation to the root from Newton's Method.

    Figure P2   `dy/dt=0.3ytext[(]3-y text[)]`	Figure P3   `dy/dt=0.3 text[(]3-t text[)]`

12. The square root of a number `A` can be calculated by solving the equation `x^2-A=0` numerically.
    1. Show that application of Newton's Method to this equation leads to a simple repeated averaging scheme. What is being averaged at each step?
    2. Start with `x_0=1`, and compute `sqrt(7)` by this scheme. Compare your result with that obtained from the square root function on your calculator or computer. Could your computing tool actually be doing repeated averaging?
    
    Note: This method for calculating square roots is sometimes called, on shaky evidence, the Babylonian method. See also Fowler and Robson, Historia Mathematica 25 (1998), 366-378.