Chapter 4
Differential Calculus and Its Uses
4.4 The Product Rule
Problems
- Given `y=text[(]1+t^2text[) (]t^3-3t^2+1text[)]`, calculate `dytext[/]dt` two ways:
- using the Product Rule.
- multiplying the two factors before differentiating.
Verify that the two answers you get are equivalent. -
- Calculate `dytext[/]dt`, where `y=text[(]1+2t text[)]e^(-3t)`.
- Check your formula for the derivative at three different values of `t` by calculating `Delta ytext[/]Delta t` for an appropriately small `Delta t`.
- Use Newton's Method to find the smaller root of `ftext[(]x text[)]=0`, where
`ftext[(]x text[)]=text[(]0.3x+2.5text[)]e^(x/2)-7x`.
- Verify that `ftext[(]0.4text[)]` and `ftext[(]0.5text[)]` have different signs. Why does this imply that the root lies between `x=0.4` and `x=0.5`?
- Set `x_0=0.4`, and verify the entries in Table P1, using your result from Checkpoint 1. Copy the table, and fill in the rest of the entries.
Table P1 Newton's Method calculation `n``x_n``ftext[(]x_ntext[)]``f'text[(]x_ntext[)]``ftext[(]x_ntext[)]//f'text[(]x_ntext[)]`00.40.400075-5.033542-0.07948210.47948223 -
 A patient's reaction `Rtext[(]x text[)]` to a drug dose of size `x` is given by a formula of the form
`Rtext[(]x text[)]=Ax^2text[(]B-x text[)]`,
where `A` and `B` are positive constants. The sensitivity of the patient's body to a dose of size `x` is defined to be `R'text[(]x text[)]`.
A patient's reaction `Rtext[(]x text[)]` to a drug dose of size `x` is given by a formula of the form
`Rtext[(]x text[)]=Ax^2text[(]B-x text[)]`,
where `A` and `B` are positive constants. The sensitivity of the patient's body to a dose of size `x` is defined to be `R'text[(]x text[)]`.
- What do you think the domain of `x` is? What is the physical meaning of the constant `B`? Of the constant `A`?
- For what value of `x` is `R` a maximum? (Your answer should contain the constant `B`.)
- What is the maximum value of `R`?
- For what value of `x` is the sensitivity a maximum?
- Why is it called “sensitivity”?
-
 Your local pizza delivery uses square boxes that are made from rectangular pieces of corrugated cardboard, each 47 by 90 cm. The box is made by cutting out six small squares, three from each of the 90-cm edges, one square at each corner and one in the middle of the edge. The result is then folded into a box in the obvious fashion. How does one design a box in this fashion to obtain the largest volume?
Your local pizza delivery uses square boxes that are made from rectangular pieces of corrugated cardboard, each 47 by 90 cm. The box is made by cutting out six small squares, three from each of the 90-cm edges, one square at each corner and one in the middle of the edge. The result is then folded into a box in the obvious fashion. How does one design a box in this fashion to obtain the largest volume? -
Figure P1 repeats the figure from Chapter 2 that depicts Thomas Malthus's view of the eventual population crisis, with population growing exponentially and food supply growing linearly. Suppose we give Malthus the benefit of the doubt on both growth rates and try to determine when the food supply would become inadequate. We set `t=0` in 1800, and we take one unit on the food scale to mean just enough food to feed the entire population in that year. The unit of population is the population in 1800; i.e., `Ptext[(]0 text[)]=1`. We interpret the food function to mean potential for producing food at a given time. If we were to zoom in on the graph, we might find that a reasonable initial value is `Ftext[(]0 text[)]=5`.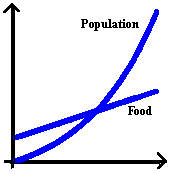 Figure P1 Malthus's view
Figure P1 Malthus's view
of population growth
Suppose the population grows at a rate of `2`% per year (compounded continuously), and the slope of the food function is `0.1`. In what year would the potential food supply be just adequate for the population? What would happen after that? In what year would the potential food surplus (relative to the population) be greatest? (Our numbers here are fictional—they should not be taken seriously.) - Which would you think is the larger term in growth rate of energy consumption — population times growth rate of per capita consumption or per capita consumption times population growth rate? Check to see how much each term contributed to the 1985 growth rate of 1.5 billion BTUs per year.

