4.5.1 Optimization in Nature

Do the following experiment: Look at a mirror, and focus on a small object that you see in the mirror. You see that object because there are light rays traveling from it to the mirror and then to your eye. Light rays normally travel in straight lines, but they can be bent — for example, by reflection in mirrors. Now visualize three points in space: the object, your eye, and the image of the object in the mirror (see Figure 1). The ray from the object to its image in the mirror makes an angle with the mirror that we label `alpha` in Figure 1. The ray from the image to your eye makes an angle we call `beta`. As you are looking in the mirror, estimate the sizes of `alpha` and `beta`. Vary your position in the room with respect to the object, and, for each new position, estimate `alpha` and `beta` again. How do you think `alpha` and `beta` are related?

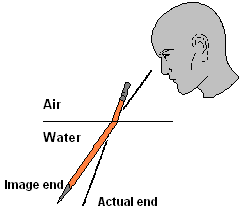
Now try this experiment. Fill a glass with water, and place a pencil in the water at an angle (not vertical). Notice the apparent bend in the pencil at the surface of the water? You know the water is not actually bending the pencil, so it must be bending the light rays from the pencil to your eye. More precisely, a light ray from a point on the pencil (say, the bottom end) travels through the water along a straight line to the surface, and then it changes direction to travel along another straight line to your eye.

We illustrate this situation in the left half of Figure 2 with the actual and apparent positions of the pencil. The heavy line is the route taken by a light ray from the end of the pencil to your eye. This bending phenomenon is called refraction, and it occurs whenever a light ray passes from one medium to another in which the speed of light is different. In the right half of Figure 2 we have labeled the angles the light ray makes with the vertical `alpha` (in water) and `beta` (in air). How do you think the angles `alpha` and `beta` in Figure 2 are related? The question is much harder for refraction than for reflection — don't worry if you can't answer it yet.

In both of our experiments, the angle we have labeled `alpha` is called the angle of incidence. For reflection, this means the angle at which the light ray meets the mirror surface. For refraction, it means the complement of the angle at which the light ray meets the water-air surface.

Note 1 - Complementary angles

The angles we have labeled `beta` are called, respectively, angle of reflection and angle of refraction. In the case of reflection, you probably have a pretty good idea from our simple experiment how `alpha` and `beta` are related, even if you have never thought about it before. In the case of refraction, it is unlikely that you can even guess the relationship — unless you remember it from a physics course.

Experiments with light rays, confirmed many times over a period of at least 300 years, suggest that light obeys a simple and plausible optimization law:

Fermat's Principle   Light follows a path that minimizes total travel time.

This principle enables us to calculate the bending of light, whether by mirrors, water-air interfaces, lenses, prisms, or rainbows. All we have to do is write down a formula for total travel time as a function of something, and find the value of "something" that gives the minimum value of the function. As we have seen earlier in this chapter, one way to do that is to calculate a derivative and find its zeros — the critical values of the total-time function. For the case of reflection, we will carry out that process in the next section. The case of refraction we leave to a Project at the end of the chapter.

Later in this section, we will find that the total distance function for reflection has the form

where `x` measures the position of the reflection point on the mirror, and `p,` `q,` and `D` are constants. Some features of this function — for example, sums and squares — are familiar. But this function has two features that we have not encountered in our previous studies of derivatives:

1. square roots

2. a composite structure.

What we mean by "composite" is this: We have not just the square of `x` but the square of `D-x` to deal with. And we have not just the square root of `x` but square roots of polynomials in `x`.

We devote the rest of this section to learning these two things:

• how to differentiate the square root function, and

• how to differentiate a composite function.

Note 2 - Source

Image credits