Problems

1. Use the Chain Rule to calculate the derivative of `text[(]1+3xtext[)]^4`. Check your answer by expanding `text[(]1+3xtext[)]^4` and differentiating term by term.
2. Suppose `z^2=x^2+y^2`, where `x`, `y`, and `z` are all functions of `t`. Find `(dz)/(dt)` in terms of `x`, `y`, `(dx)/(dt)`, and `(dy)/(dt)`.
3. In Section 2.6 we studied exponential growth as a model for growth of a colony of fruit files. For reasons we will see later, a more reasonable model for the growth data for such a colony is the logistic growth equation,

   `(dP)/(dt)=cP(M-P)`,

   where `Ptext[(]t text[)]` is the population at time `t`, `M` is the maximum supportable population of the environment, and `c` is a proportionality constant. In brief, when `P` is very small relative to `M`, the factor `M-P` is almost constant, and the early growth is exponential. But when `P` gets close to `M`, the factor `M-P` is close to `0`, and the colony stops growing.
   1. Explain why the population must be growing most rapidly at a time at which the second derivative of `P` is zero.
   2. Differentiate both sides of the differential equation to find an expression for the second derivative. (The Product Rule works for differentiating the right-hand side, but you can make the computation easier if you rewrite the expression in another form first.) Be careful with your differentiation — you are differentiating with respect to `t`, not `P`, so the Chain Rule must come into play every time you run into the unknown function `P`.
   3. What does your expression for the second derivative tell you about the population size when the growth rate is maximal?
4. When a drug is injected into the bloodstream, its concentration `Ctext[(]t text[)]` at `t` minutes after injection is given by a formula of the form

   `Ctext[(]t text[)]=K (e^(-bt)-e^(-at))/(a-b)`,

   where `K`, `a`, and `b` are positive constants, and `a>b`. When does the maximum concentration occur?
   
   This problem is adapted from Five Applications of Max-Min Theory from Calculus, by W. Thurmon Whitley, UMAP Module 341, COMAP, 1979.
5. 

   1. What is the cone of largest volume that can be formed by rotating a right triangle of fixed hypotenuse `h ` around one of its legs?
   
   
   2. What is the volume of that cone?

 

6. 1. Write down formulas for two even functions. Sketch the graph of each of these functions. Sketch the graph of the derivative of each of these functions. (You may use your graphing tool.)
   2. Write down formulas for two odd functions. Sketch the graph of each of these functions. Sketch the graph of the derivative of each of these functions.
   3. What conclusion(s) do you draw from parts (a) and (b)?
7. If `y=ftext[(]utext[)]` and `u=gtext[(]xtext[)]`, then `y=ftext[(]gtext[(]xtext[))]`. The function `ftext[(]gtext[(]xtext[))]` is called the composite of `f` and `g`. For example, if `ftext[(]utext[)]=u^2` and `gtext[(]xtext[)]=x^3+x`, then `ftext[(]gtext[(]xtext[))]=text[(]x^3+xtext[)]^2`. What can be said about the oddness or evenness of the composite of `f` and `g` if
   
   
   1. `f` and `g` are both odd?
   2. `f` and `g` are both even?
   3. `f` is odd and `g` is even?
   4. `f` is even and `g` is odd?
      
      
   Give an example for each of the cases in parts (a) through (d). Verify that the composite in each case has the oddness or evenness property you said it should have.
   
   This problem is adapted from Calculus Problems for a New Century, edited by Robert Fraga, MAA Notes No. 28, 1993.
8. 1. Explain in geometric terms (i.e., by using symmetries and slopes) why the derivative of an odd function is an even function and why the derivative of an even function is an odd function. (See Example 3 in Section 4.1, Activity 1 in Section 4.2, and Problem 6 for examples that illustrate both these statements.)
   2. Explain in algebraic terms (i.e., by using difference quotients) why the derivative of an odd function is an even function and why the derivative of an even function is an odd function.
   3. Explain in calculus terms (i.e., by using the Chain Rule) why the derivative of an odd function is an even function and why the derivative of an even function is an odd function.
9. Develop the following argument to establish the Product Rule by using the Chain Rule and without resorting to difference quotient calculations.
   1. Let `x=xtext[(]t text[)]` and `y=ytext[(]t text[)]` be any two functions. Expand the square `text[(]x+ytext[)]^2` to find an equal expression in terms of `x^2`, `y^2`, and `xy`.
   2. Solve your equation for `xy`.
   3. The other side of the equation now contains only squares of unknown functions, which you can differentiate with the aid of the Chain Rule. Thus, when you differentiate both sides, you should find an expression for the derivative of `xy` with respect to `t`. With any luck (skill?), your expression will turn out to be the Product Rule.
10. We show typical graphs of `Ltext[(]xtext[)]` and `L'text[(]xtext[)]` again in Figure E1, repeated from Figure 4.
    1. It is clear from this figure that `Ltext[(]xtext[)]` also has a maximum value on the interval `0<=x<=D` — and it does not occur at a point where `L'text[(]xtext[)]=0`. Where does it occur?
    2. Recall that

       `Ltext[(]xtext[)]=sqrt(p^2+x^2)+sqrt(q^2+(D-x)^2)`

       for any `x` between `0` and `D`. Does your answer to part (a) depend on the relative sizes of `p` and `q`? If so, how?

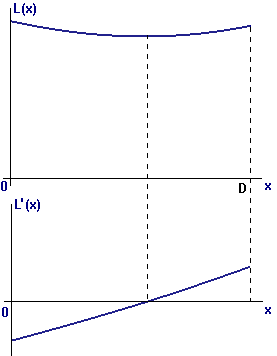
    Figure E1   L(x) and its derivative

11. A square plot of ground 100 feet on a side has corners that we label `A`, `B`, `C`, and `D` clockwise. Pipe is to be laid in a straight line from `A` to a point `P` on the side `BC` and thence to `C`. (`P` could be one of the corners `B` or `C`.) The cost of laying the pipe is `\$50` a foot if it goes through the lot (because it must be laid underground) and `\$25` a foot if it is laid along one of the sides of the square. What is the most economical way to lay the pipe?
    
    This problem and the next one are adapted from Calculus Problems for a New Century, edited by Robert Fraga, MAA Notes No. 28, 1993.
12. Lee and Dana are in a rowboat half a mile from the nearest point on a relatively straight shoreline when Dana suddenly becomes ill. The closest place to find a telephone to call for help is at a seaside restaurant 1 mile from the nearest point on shore. Lee plans to row to a point on the shore and then jog to the restaurant. Lee can jog at 6 miles per hour and row at 1.5 miles per hour.

    1. How long would it take to get to the restaurant if Lee rows to the nearest point on shore?
    2. How long would it take if Lee rows directly to the restaurant?
    3. What point on the shore would make the trip to restaurant as quick as possible? How long would it take to get to the restaurant?
    4. How fast would Lee have to row so that the quickest route would be to row directly to the restaurant?
13. Print a copy of Figure 3, and add to the figure the point `P'` at which the point `P` appears to be (behind the mirror) when your eye is at `Q`. Use a shortest-distance-between- two-points argument and elementary geometry to explain why `alpha` and `beta` must be the same angle.
14. A mirror is placed flat on the ground 7 meters from the base of a tree. When a person whose eyes are 180 centimeters from the ground stands 1 meter beyond the mirror, he or she can see the top of the tree in the mirror. How tall is the tree?