Chapter 4
Differential Calculus and Its Uses
4.6 Derivatives of Functions Defined Implicitly
4.6.1 An Example
In Figure 1 we graph the ellipse with equation
Suppose we want to know the slope of the tangent line to the ellipse at the point `text[(]x_0,y_0text[)]`, where `x_0=1` and `y_0=3sqrt(3)text[/]2~~2.598`.
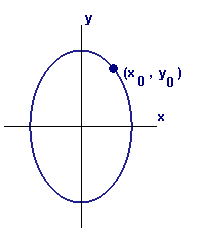
Figure 1 Graph of
One approach would be to find an explicit description `y=ftext[(]xtext[)]` for the top half of the ellipse, differentiate that function, and evaluate the derivative at `x=1`. You will carry out that computation later in Checkpoint 1.
However, before you do that, let's consider another approach. Whatever the functional relation between `y` and `x`, for each value of `x` we know that
Thus the function of `x` on the left side, obtained by squaring `y`, dividing by `9`, and adding `x^2text[/]4`, must be the same function as the one on the right side, i.e., the function on the left must be the constant function `1.`
Now we differentiate both the left-hand and the right-hand functions. On the left, we use the Sum Rule, the Power Rule, and the Chain Rule to obtain
On the right, the derivative of the constant `1` is `0`. Since the two derivatives are equal, we may write
We solve for `dytext[/]dx` to find
In particular, at `x_0=1` and `y_0=3sqrt(3) text[/]2`, we find
The ellipse in Figure 1 combines the graphs of two functions of the form `y=ytext[(]xtext[)]`, one for the top half of the ellipse and one for the bottom half. Both of those functions are defined implicitly by the equation of the ellipse,
Our technique for calculating `dytext[/]dx` directly from the implicit definition applies to both functions.


