Chapter 4
Differential Calculus and Its Uses
4.6 Derivatives of Functions Defined Implicitly
4.6.2 The Derivative of the Natural Logarithm
We have formulas for the derivatives of all but one of the functions we have encountered so far — all except the natural logarithm. Before we find this formula, let's return to the definition of the derivative and look at difference quotients for `ln x`.
In Figure 2 we graph the difference quotient function
which should closely approximate the derivative of `ln x`. Do you recognize this function?
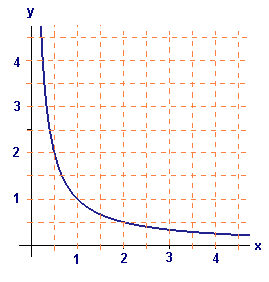
Figure 2 Graph of the difference quotient for ln x
Activity 1
-
Use the graph to estimate the difference quotient for `x=1text[/]4`, `x=1text[/]2,` `x=1`, `x=2`, and `x=4`.
On the basis of your estimates in (a), make a conjecture about the derivative of `ln x`.
Now let's find the formula for the derivative of `ln x` (and, we hope, verify your conjecture). Implicit differentiation turns out to be just what we need. If `y=ln x`, then, by the definition of the natural logarithm, `e^y=x.` If we differentiate both sides of this equation with respect to `x`, we obtain
which leads to
But, since `e^y=x`, we find
We have shown that
Since the natural logarithm is defined only for positive numbers `x`, this formula is correct for all `x>0`.
Implicit differentiation is a useful way to obtain differentiation formulas. In Example 1 we use this method to derive again the formula we know already for the derivative of the square root function.
Apply the implicit differentiation technique to the equation
to obtain the formula
Solution Differentiating both sides of the equation `y^2=x` with respect to `x`, we find
Solving for `dytext[/]dx`, we get
Since `y=sqrt(x)`, we may substitute to obtain



