Chapter 4
Differential Calculus and Its Uses
4.7 The General Power Rule
4.7.3 Power Functions with Irrational Exponents
We turn now to the question of what might be meant by `t^(pi)` or `t^sqrt(2)` or `t^sqrt(pi)` or `t^(-pi//4)`. When we can answer that question, we will also see that we can calculate the derivatives of such functions with rules that are mostly known to us already. Even though the techniques will turn out to be different from the algebraic calculations we have done already, the answer will be the same — the Power Rule.
We can sneak up on `t^(pi)` by considering a sequence of rational approximations to `pi`, namely, the successive decimal approximations to `pi`:
Each number in this list is rational, i.e., is the ratio of two integers. Thus, at least for positive values of `t`, it makes sense to use each of these numbers as an exponent on `t`. For example, `t^(3.14)` means the same thing as `t^(314//100)`, which can be interpreted as the `100`-th root of the `314`-th power of `t`. The next number in the list, `t^(3.141)`, means the same things as `t^(3141//1000)` or the `1000`-th root of the `3141`-th power. The restriction that `t` be positive is necessary to make sense out of the general root step in the interpretations just given.
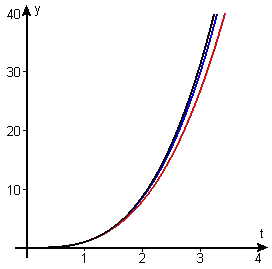
Now that we understand what is meant by an exponent that is a decimal fraction, we consider the graphs of
`t^3, t^(3.1), t^(3.14), t^3.141,` and `t^3.1415`,
all of which are shown in Figure 1. Because each exponent is slightly larger than the one before, the order on the graph is bottom to top. For the interval shown in Figure 1, only the first two of these power functions are visually distinct from the last.
Figure 1 Successive power functions approximating `t^pi`
Activity 3
Click on the graph in Figure 1 to bring up an animated version that shows successively the graphs of `y=t^3`, `y=t^(3.1)`, `y=t^(3.14)`, `y=t^(3.141)`, `y=t^(3.1415)`, and finally a computer's interpretation of `y=t^(pi).` Repeat as necessary until you are clear about what changes each time the exponent gets a little larger.
The power functions — the ones shown in the animation and all the later ones determined by longer decimal approximations to `pi` — are distinct, but the differences between them quickly get smaller and smaller, which suggests that there is a limiting function that the power functions approach as the powers get closer to `pi`. That limiting function is what we call `t^(pi)`. When we added the graph of `y=t^(pi)` to the others, we could see no change in the figure — the limiting function is visually indistinguishable from the last power function shown.
Activity 4
Write out formulas for the derivatives of each of the following functions:
You know how to do this because each of the exponents is a rational number. Now explain in your own words why
