Problems

1. Use implicit differentiation to show that the Power Rule holds for the derivative of `x^(5//3)`.
2. Use implicit differentiation to show that the Power Rule holds for the derivative of `x^(9//2)`.
3. Write an operational definition of `t^3.14159` in terms of integer powers and roots.
4. 1. Calculate the derivatives of the two functions `e^x` and `x^e`.
   2. Use your graphing tool to plot the graphs of `e^x` and `x^e` on the interval from `0` to `4`.
   3. Do the two graphs in part (b) intersect? Do they cross?
   4. Plot the graphs of the derivatives of the two functions over the same interval. Find the values of `x` where these two graphs cross.
   5. What is the geometric significance for the graphs of `e^x` and `x^e` of values of `x` where the derivative graphs cross?
5. A rectangular computer chip is made of ceramic material with circuitry placed in an interior rectangle. Two parallel edges of the circuitry are each 1 millimeter from the corresponding edge of the chip, and the other two edges are each 2 millimeters from the corresponding edges of the chip. How should a chip whose area is 200 square millimeters be designed in order to maximize the area of the circuitry it can accommodate?
6. In a recent (fictional) study, scientists formulated the following equation to represent the amount `i` of information retained from one day of studying:

   `i=k s c^(3//2)`,

   where `s` is the number of hours slept, `c` is the number of hours spent cramming, and `k` is a proportionality constant. Assuming that the average freshman prepares for finals by cramming every hour that she or he is not sleeping, how much should a student sleep in the course of a day to maximize the knowledge retained? Justify that your answer yields a maximum.

7. We gave meaning to the expression `t^pi` as a function by treating it as a limiting function obtained from successive rational approximations to `pi`. Since we knew the Power Rule applied to rational powers of `t`, we were able to show (Activity 3) that the Power Rule also applies to this irrational-power function. With the aid of the Chain Rule and the rule for differentiating the natural logarithm function, you can show that the Power Rule applies to all power functions:
   1. Explain why `t^r` must be the same thing as `e^(r ln t)` for every pair of positive real numbers `t` and `r`, regardless of what's variable and what's constant.
   2. Now suppose `t` is the independent variable and `r` is a constant. Explain why the function `y=t^r` is the same as `y=e^u`, where `u=r ln t`.
   3. Use the Chain Rule to find `dytext[/]dt`, and simplify to show that the result is the same as the Power Rule.
8. Let `f` be the function defined by `ftext[(]xtext[)]=x^x`.
   1. Sketch the graph of `f`.
   2. Find a formula for `f'text[(]xtext[)]`. (Hint: `y=x^x` satisfies the equation `ln y=x ln x`.)
   3. Find the smallest value of `x^x`.
9. In Figure E1 we show again the graphs of `Ltext[(]xtext[)]`, the length of path for a reflected ray as a function of where the ray would hit the mirror, and its derivative `L'text[(]xtext[)]`.

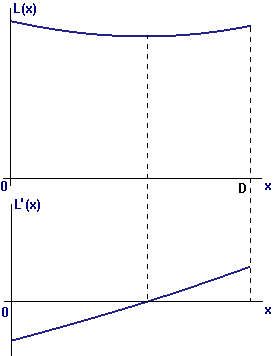
   Figure E1   L(x) and its derivative

   Here again are the formulas for `Ltext[(]xtext[)]` and `L'text[(]xtext[)]`:

   `Ltext[(]xtext[)]=sqrt(p^2+x^2)+sqrt(q^2+(D-x)^2)`

   and

   `L'text[(]xtext[)]=x/(sqrt(p^2+x^2))+(x-D)/(sqrt(q^2+(D-x)^2))`

   for any `x` between `0` and `D`.

   1. Find the second derivative of `Ltext[(]xtext[)]`, and show that it is always positive. [Hint: See Exercise 2(c). The `p`-term and the `q`-term of `L'` each produce two terms in the derivative. Combine each pair by using a common denominator, and you should find that each numerator must be positive.]
   2. Explain why the minimum value of `Ltext[(]xtext[)]` must occur at the only `x` that satisfies `L'text[(]xtext[)]=0`.
10. 1. Derive a Quotient Rule for differentiation. Let `ftext[(]t text[)]` and `gtext[(]t text[)]` be any two functions, and find a way to express the derivative of `ftext[(]t text[)/]gtext[(]t text[)]` in terms of the derivatives of `ftext[(]t text[)]` and `gtext[(]t text[)]`. [Hint: Write the quotient as `ftext[(]t text[)] gtext[(]t text[)]^(-1)`.]
    2. Use your rule to find the derivative of `(t^2+1)/e^t`.
    3. Write the function in part (b) as `(t^2+1) e^(-t)`, and confirm that you get the same answer for the derivative by using the Product Rule.
11. Calculate the derivative of each of the following functions.

    a.

    `t^(2//3)/(1+t^2)`

    b.

    `(1+t^2)/t^(2//3)`

    c.

    `(ln t)/(1+t^(1//3))`