Exercises

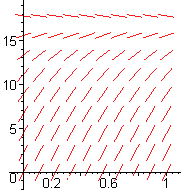
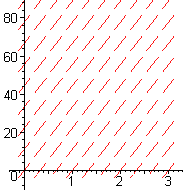
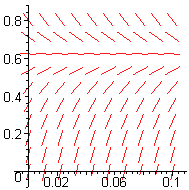
1. Figure E1 shows the slope fields for velocity, according to the Galileo, Stokes, and Velocity-Squared models, not necessarily in that order. Explain which is which and why.

Figure E1   Raindrop slope fields

2. In Checkpoint 3 of Section 3.3 you determined that a marble dropped from a height of `535` feet, according to Galileo's Model (no air resistance), would hit the ground at `127` miles per hour. In this section, we computed that a raindrop falling from `3000` feet — if it were a marble — would hit the ground at about `300` MPH.

   1. Find a formula for the time of fall, according to Galileo's Model, from an arbitrary height `h`.
   2. Find a formula for the speed at impact in miles per hour. (Be careful with units.)
   3. Use the two cases we have computed already to check your formula.
   4. Use your formula to find the speed at impact for a fall from `10` feet; `100` feet; `1000` feet; `10text[,]000` feet.
3. In Activities 2 and 3, you determined the basic facts for a falling object whose drag (air resistance) is proportional to velocity with proportionality constant `k`: The terminal velocity `v`_term is `g`/`k`, and the velocity at time `t` is

`v text[(]t text[)]=v`_term`(1-e^(-kt))`.

1. Find a formula for the time to reach 99% of terminal velocity, in terms of `k`.
2. Check your formula with the case you already know, the drizzle drop for which `k=0.329/D^2 times 10^(-5) sec^(-1)` and `D=0.00025` feet.
3. What would `k` have to be in order to take one hour to reach `99text[%]` of terminal velocity?
4. Suppose resistance is proportional to `sqrt(v)`, as might be the case for a small object falling through a viscous fluid. Find an expression for the terminal velocity in terms `g` and the proportionality constant `k`.
5. Pilots and parachutists know (and physicists confirm) that the Velocity-Squared Model applies to the resisting force of air on an airplane wing or a falling human body, with or without a parachute. Thus, the acceleration equation has the form `dv text[/] dt=g-c v^2`. Ms. Jennifer Phillips of Orange, MA, an experienced sky diver, reports the following free fall terminal velocities:

   1. `170` mph in fetal position,
   2. `140` mph in a nose dive,
   3. `120` mph in a horizontal position with arms and legs spread out.

   For each of these cases, find the proportionality constant `c`.

Note 2 – Sources

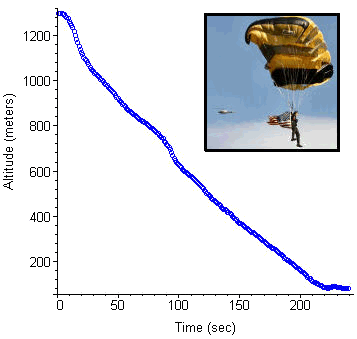
6. The photo inset in Figure E2 shows a member of the US Military Academy's Black Knights Parachute Team jumping from a helicopter into Michie Stadium. The graph in Figure E2 shows the jumper's altitude as a function of time, as recorded by a GPS device carried on the jump.

   Click on Figure E2 to see a Quicktime movie of the last 90 seconds of the parachute drop. (9 MB download)

   Figure E2   Recorded altitudes for a parachute jump

   Note that, after the parachute opens at about 20 seconds, the altitude changes almost linearly, that is, at a constant (terminal) velocity.

   1. Use a computer algebra tool to fit a line to the "straight" part of the graph, and thereby determine the terminal velocity, both in meters per second and miles per hour.
   2. Determine the proportionality constant `c` in the Velocity-Squared Model, `dv`/`dt=g-c v^2`.

Note 3 – Source and additional information

7. In Figure E3, we zoom in on the first 20 seconds of the parachute jump in Exercise 6.

   Figure E3   Recorded altitudes for the start of a parachute jump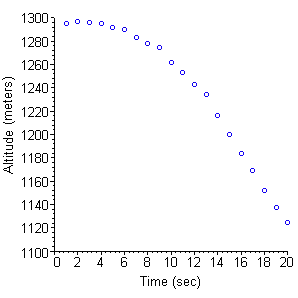

   The chute opened at about 19 seconds, but for several seconds before that, the jumper was falling at terminal velocity for his position with the chute not yet open.

   1. Use your computer algebra system to find that pre-parachute terminal velocity.
   2. For the brief free-fall period before the parachute opened, determine the proportionality constant `c` in the Velocity-Squared Model, `dv`/`dt=g-c v^2`.
   3. How does the free-fall terminal velocity compare with the skydiving velocities in Exercise 5? Can you explain the differences (if any)?