Chapter 5
Modeling with Differential Equations





5.3 Periodic Motion

5.3.3 Circular Motion: Sines and Cosines

Imagine a circular running track of radius one hundred meters, and imagine an `xy`-coordinate system placed on the track with the center of the circle at the origin. (See Figure 3.) Suppose you start at the point with coordinates `x=100` and `y=0` and run in a counterclockwise direction with a speed of five meters per second. How can we describe your position as a function of the angle `theta` between your line to the origin and the `x`-axis? How can we describe your position as a function of time?

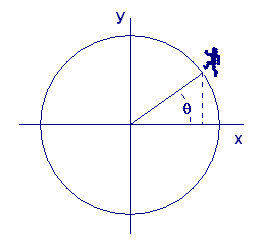Figure 3   Position of a runner on a track of 100 meters

Consider first the question of describing your position in terms of `theta`. We'll measure the angle in radians, so one lap corresponds to `2pi` radians, a quarter lap to `pitext[/]2` radians, and so on. To locate your position in the plane, we need to specify both the `x`- and `y`-coordinates. The functions that do this should be old friends — or at least passing acquaintances. If you have traveled through an angle of `theta` radians, then you are located at the point with `x`-coordinate `100 costext[(]theta text[)]` meters and `y`-coordinate `100 sintext[(]theta text[)]` meters. That is,

x = 100 ⁢   cos ( θ ) ,

and

y = 100   sin ( θ ) ⁢ .

Checkpoint 1 Checkpoint 1

In Figure 4, we show another circle of radius `100` with separate graphs of the `x`- and `y`-coordinates (as functions of the central angle `theta`) that result from motion around the circle.

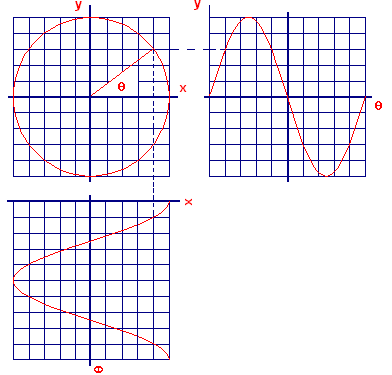Figure 4   Generation of sine and cosine functions from motion around a circle

Notice that the axes for the `x`-coordinate graph are rotated `pitext[/]2` radians (90°) clockwise from the usual position. In Figure 5 we show the left half of Figure 4 rotated counterclockwise `pitext[/]2` radians.

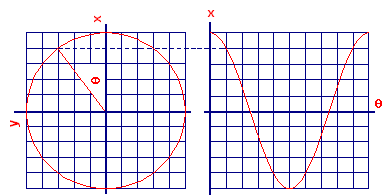Figure 5   Generation of cosine function from motion around a circle

Activity 2

  1. With Figure 4 on the screen, put the index finger of your left hand on the circle at the point `text[(]100,0text[)]` and the index finger of your right hand on the graph of the `y`-coordinate at the point `text[(]0,0text[)].` As you move your left finger along the circle, let your right finger trace out the graph of `y` as a function of `theta.`
  2. With Figure 5 on the screen, place your left index finger at the point `text[(]0,100text[)]` on the `x`-coordinate graph and your right index finger on the circle at the point `text[(]100,0text[)].` As you move your left finger along the circle, let your right finger trace out the graph of `x` as a function of `theta.`

You have just experienced the generation of the sine and cosine functions from motion around a circle.

Checkpoint 2 Checkpoint 2

Now we turn to the question of your location on the track as a function of time in seconds. Let `t=0` correspond to your starting position at `x=100` and `y=0.` Answer the questions in Checkpoint 3 and find the formulas requested.

Checkpoint 3 Checkpoint 3

Activity 3

  1. What circle is traveled by a moving object with coordinate functions `x=costext[(]thetatext[)]` and `y=sintext[(]thetatext[)]`? (This circle is called the unit circle.)

Explain the following facts about sine and cosine:

  1. For every angle `theta`, `costext[(]theta + 2 pitext[)]=costext[(]thetatext[)].`

  2. For every angle `theta`, `sintext[(]theta + 2 pitext[)]=sintext[(]thetatext[)].`

  3. For every angle `theta`, `sin^2text[(]thetatext[)]+cos^2text[(]thetatext[)] =1.`

  4. For every angle `theta`, | sin ( θ ) | ≤ 1.

  5. For every angle `theta`, | cos ( θ ) | ≤ 1.

Comment 3Comment on Activity 3

Checkpoint 4Checkpoint 4

Image credit
Go to Back One Page Go Forward One Page

Go to Contents for Chapter 5Contents for Chapter 5