Exercises

1. Solve each of the following initial value problems.

   `(dy)/(dt)=1.3y`, `ytext[(]0text[)]=-0.5`
   `(dy)/(dt)=-1.3y`, `ytext[(]0text[)]=0.5`
   `(d^2y)/(dt^2)=-1.3y`, `ytext[(]0text[)]=-0.5`, `y'text[(]0text[)]=0`
   `(d^2y)/(dt^2)=-1.3y`, `ytext[(]0text[)]=0`, `y'text[(]0text[)]=-0.5`

2. Solve the initial value problem `(d^2y)/(dt^2)=-1.3y`, `ytext[(]0text[)]=-0.5`, `y'text[(]0text[)]=0`. (Hint: Find two exponential functions, `e^(rt)` and `e^(st)`, that satisfy the differential equation. Then look for a solution of the initial value problem of the form `A e^(rt)+B e^(st)`.)
3. 1. What is the frequency of the oscillation of a spring-mass system with mass `m` and spring constant `k`?
   2. What is the period?
4. The frequency of household electric current is 60 hertz. (One hertz is one cycle per second.) If this current is described by a formula of the form `x text[(]t text[)]=A sin omega t+B cos omega t`, and time is measured in seconds, what is `omega text[?]`
5. The clock speed of a certain personal computer is 1.6 gigahertz. If the oscillation is described by a formula of the form `xtext[(]t text[)]=A sin omega t+B cos omega t`, and time is measured in microseconds, what is `omega`? (The prefix giga- means one billion, and the prefix micro- means one-millionth.)
6. If the mass attached to a spring is thrown (vertically up or down) instead of let go, all that changes in our initial value problem is that the initial velocity is no longer zero.
   1. The initial velocity can be either positive or negative. Which sign corresponds to throwing the mass up and which down?
   2. Find values for the constants `A` and `B` such that the function

      `xtext[(]t text[)]=A sin(sqrt(k/m) t)+B cos(sqrt(k/m) t)`

      satisfies the initial value problem

      `(d^2x)/(dt^2)=-k/mx,`   with  `xtext[(]0text[)]=1`  and  `x'text[(]0text[)]=-0.5`.

7. Interpret the initial value problem

   `(d^2y)/(dt^2)=-1.07y,`   with  `ytext[(]0text[)]=-0.5`  and  `y'text[(]0text[)]=0.5`

   as representing the motion of a spring-mass system. What are the mass and the spring constant? What is the initial state of the system?
8. A mass of 4 kilograms is suspended from a spring attached to the ceiling that has a spring constant of 9 kilograms per second squared. The mass is pulled downward 1 meter below its equilibrium position and then released from this point with an initial velocity upward of 1.5 meters per second.
   1. Write down the differential equation and initial conditions satisfied by the function `xtext[(]t text[)]` that gives displacement of the mass from equilibrium as a function of time.
   2. Solve the initial value problem to find `xtext[(]t text[)]`.
   3. At what times will the mass be closest to the ceiling?
9. 1. Sketch the graph of `costext[(]2t text[)]` for `0<=t<=2pi`.
   2. Sketch the graph of `cos^2t` for `0<=t<=2pi`.
   3. Use the identities

      `cos 2t=cos^2t-sin^2t`  and  `cos^2t+sin^2t=1`

      to show that

      `cos^2t=(1+cos 2t)/2`

      for all `t`.
   4. Find all the points of inflection on the curve `y=cos^2t`, and mark them on your graph in part (b). Why must these points also be points of inflection for the curve `y=sin^2t`?
   5. Sketch the graph of `sin^2t` for `0<=t<=2pi`.
   6. Show that

      `sin^2t=(1-cos 2t)/2`

      for all `t`.
10. An airplane is flying directly overhead at an altitude of 20,000 feet. One minute later, the line of sight to the airplane makes an angle of 49 degrees with the ground. What is the approximate speed of the airplane in miles per hour?
11. A paper in the journal Statistics and Medicine reported on efforts to find baseline models for normal biological rhythms, such as the sleep-wake cycle, hormone levels, and core body temperature. The goal of such research is to be able to diagnose conditions such as depression by measuring disturbances in these rhythms. The principal example in the paper is based on temperature data gathered over a 5-day period from a healthy 28-year-old female. An embedded temperature probe recorded core body temperature every 2 minutes. The researchers used every tenth data point, so their time unit was 20 minutes. On that scale, they found the primary rhythm to be modeled quite well by a function of the form

    `ftext[(]t text[)]=mu+A cos(2pi omega t)+B sin(2pi omega t)`,

    where `mu=37.5`, `omega=0.0138`, `A=-0.103`, and `B=-0.429`.
    1. Graph the model function.
    2. What is the physiological significance of `mu`?
    3. What is the physiological significance of `omega`?
    Source: J. B. Greenhouse, R. E. Kass, and R. S. Tsay, “Fitting Nonlinear Models with ARMA Errors to Bioogical Rhythm Data,” Statistics and Medicine 6 (1987), pp. 167–183.

12. Figure E1   Approximate fit
    to minutes-of-sunlight
    data for Frederick, MD

    Figure E1 shows an approximate fit to the minutes-of-sunlight data in Activity 2. Note that the curve does not pass exactly through all of the data points. One measure (not the only one) of how well a model fits is the size of the largest relative error. At each data point `[t,y]`, there is an absolute error of `|ftext[(]t text[)]-y|`, where `f` is the model function. The relative error at that point is `|ftext[(]t text[)]-y|//|y|`. For your model function in Activity 2, find the relative error at each of the 12 data points, and determine the largest relative error. (Adapt your computer algebra tool from Activity 2 for this purpose.) Would you consider this error "large", "small", or somewhere between? Why?
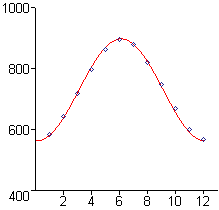
13. Figure E2 repeats Figure 1 in this section, showing monthly averages of numbers of minutes after midnight for sunrise (blue) and sunset (red) in Frederick, MD.

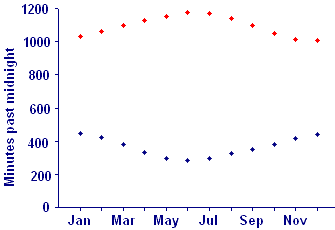
    Figure E2   Average monthly sunrise and sunset in Frederick, MD

    1. Would you expect that either or both of these data curves could be modeled adequately by a function of the form `f text[(]t text[)]=A+B sin(C text[(]t-D text[)])`? Why or why not?
    2. Adapt your computer algebra tool from Activity 2 to find as good a fit as you can to the sunrise data.
    3. Find the largest relative error for your fit to the sunrise data. (See Exercise 12.)
    4. Repeat part (b) for the sunset data.
    5. Repeat part (c) for the sunset data.
    6. How do your answers to parts (c) and (e) affect your answer to part (a), if at all?
14. Activity 2 was based on data from the US Naval Observatory, whose Astronomical ApplicationsWeb site provides data for sunrise/sunset, moonrise/moonset, or beginning/end of twilight for any location on the Earth. Select a location other than Frederick, MD, download one or more data sets, and explore whether your data can be modeled by a function of the form `ftext[(]t text[)]=A+B sin(Ctext[(]t-D text[)])`.
15. In Activity 4, we found that all solutions of `y''=-omega^2y` are all of the form `y=A sin omega t+B cos omega t`.
    1. For each such function, explain why `B` is the value of the function at `t=0`.
    2. How is `A` related to the value of the first derivative `t=0`?
16. We discovered in Chapter 2 that solutions of `y'=ky` are all of the form `y=Ae^(kt)`, and we discovered in this section that solutions of `y''=-omega^2y` are all of the form `y=A sin omega t+B cos omega t`. Now we seek solutions of `y''=omega^2y`.
    1. Show that `e^(omega t)` and `e^(-omega t)` are both solutions of `y''=omega^2y`.
    2. Show that all functions of the form `Ae^(omega t)+Be^(-omega t)`are solutions.
    3. If `omega=2`, find a solution that satisfies the initial conditions `ytext[(]0text[)]=1` and `y'text[(]0text[)]=0.5`. Check your work by substituting your solution back into the differential equation and also checking the initial conditions.
17. The solutions of `y''=omega^2y` (see Exercise 16) can be written in another form that is more suggestive of the parallel with trigonometric functions (also called circular functions). This other form uses so-called hyperbolic functions, the hyperbolic sine (abbreviated sinh) and hyperbolic cosine (abbreviated cosh). These functions may be defined from exponential functions by the following formulas:
    `sinh omega t=1/2(e^(omega t)-e^(-omega t))` and `cosh omega t=1/2(e^(omega t)+e^(-omega t))`
    1. How are the first derivatives of these hyperbolic functions related to the functions themselves?
    2. Explain why you already know that `sinh omega t` and `cosh omega t` are solutions of `y''=omega^2y`.
    3. Explain why every function of the form `A sinh omega t+B cosh omega t ` is also a solution of the same differential equation.
    4. Why must `B` be the value of such a function at `t=0`?
    5. How is `A` related to the value of the first derivative at `t=0`?
    6. Compare what you did in parts (c)-(e) with what you did in Activity 4 and Exercise 15.
    7. If `omega=2`, find a solution expressed in hyperbolic functions that satisfies the initial conditions `ytext[(]0text[)]=1` and `y'text[(]0text[)]=0.5`. Is this the same solution you found in the preceding exercise? Why or why not?
18. You showed in Activity 3 in Section 5.3 that the circular functions `x=cos omega t` and `y=sin omega t` satisfy the equation `x^2+y^2=1` — the equation of a circle — which is not surprising, given the origins of these functions in a circle.
    1. Find a similar equation satisfied by the hyperbolic functions, `x=cosh omega t` and `y=sinh omega t`. (Hint: Calculate the squares of the hyperbolic sine and the hyperbolic cosine directly from their definitions in the preceding problem.)
    2. Why are these functions called hyperbolic?
19. 1. Make a sketch, on a single set of coordinate axes, of the graphs of `y=e^x` and `y=e^(-x)`.
    2. The function `y=cosh x` is the average of the two functions whose graphs you just sketched. Sketch the average of the two graphs to find the graph of `y=cosh x`.
    3. Construct the graph of `y=sinh x` in a similar manner, as the average of two exponential graphs.
    4. Check your work with your graphing tool (which should know the names sinh and cosh).