5.5.2 Derivative of the Tangent Function

In Figure 7 we show again the graph of the tangent function. We can make some observations right away about the derivative of this function:

• It must always be positive.
• Its values must become arbitrarily large near odd multiples of `pi text[/] 2.`
• It must have a smallest positive value at integer multiples of `pi.`
• It must have the same period as the tangent function, namely, `pi.`

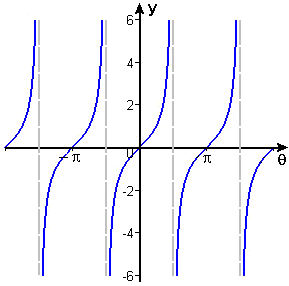
Figure 7   y = tan q

Example 2

Calculate `d/(d theta) tan theta.`

Solution   We can write `tan theta` as a product, `text[(]sin theta text[)]times text[(]cos theta text[)]^(-1),` and then apply the Product Rule (and other rules):

d d ⁢ θ ⁢ tan ( θ )	= d d ⁢ θ ⁢ sin ( θ ) [ cos ( θ ) ] - 1
	= ⁢ sin ( θ )   d d ⁢ θ [ cos ( θ ) ] - 1 ⁢ + [ cos ( θ ) ] - 1   d d ⁢ θ ⁢ sin ( θ )
	= ⁢ sin ( θ )   ( - 1 ) [ cos ( θ ) ] - 2 ⁢ [ - sin ( θ ) ] + [ cos ( θ ) ] - 1   cos ( θ )
	= sin 2 ( θ ) cos 2 ( θ ) ⁢ + 1
	= tan 2 ( θ ) ⁢ + 1.

Checkpoint 2

Activity 4

Now that we have a formula for the derivative of the tangent function, confirm from the formula each of the observations at the top of this page:

1. `tan^2 theta + 1` is always positive.
2. The values of `tan^2 theta + 1` are arbitrarily large near odd multiples of `pi text[/] 2.`
3. `tan^2 theta + 1` has its smallest positive value at integer multiples of `pi.` What is that smallest value?
4. `tan^2 theta + 1` has the same period as the tangent function, namely, `pi.`
5. Use the information in parts (a)-(d) to sketch a graph of the derivative of the tangent function — freehand, on a sheet of paper.

Comment on Activity 4

The formula for the derivative of the tangent function is usually not written in the form `tan^2 theta + 1.` You may — or may not — recall a trigonometric identity that relates this expression to another trigonometric function, the secant. You should recall that the secant is the reciprocal of the cosine:

sec ( θ ) = ⁢ ⁢ 1 cos ( θ ) .

Activity 5

Show that

`d/(d theta) tan theta = sec^2 theta.`

In other words, establish the identity

`tan^2 theta + 1 = sec^2 theta.`

Comment on Activity 5