5.5.3 Inverse Trigonometric Functions

We repeat here the graphs of two of our trigonometric functions, sine and tangent.

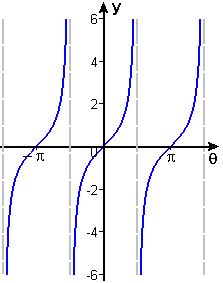Figure 8   `y = sin q`	Figure 9   `y = tan q`

It is immediately evident from the graphs that neither of these functions has an inverse function, because neither can pass the "horizontal line test" — that is, for a given `y` value (in the range of the function), there is more than one `theta` value. Indeed, every periodic function of `theta` has infinitely many `theta` values for each `y` value — and therefore cannot have an inverse function. Now, this may fly in the face of your past experience, because you are surely familiar with the phrase "inverse trig function" — your calculator even has buttons for such functions.

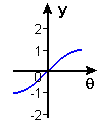
As we saw in Chapter 1 with the squaring function, the secret to defining inverse trig functions is to reduce their respective domains to ones in which each `y`-coordinate occurs exactly once. For the sine function, this is accomplished by using the domain `-pi text(/) 2 <= theta <= pi text(/) 2,` and for tangent, we use the open interval `-pi text[/] 2 < theta < pi text[/] 2.` These restricted-domain functions are shown in Figures 10 and 11.

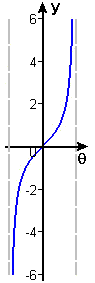Figure 10   y = sin q, -p/2 ≤ q ≤ p/2	Figure 11   y = tan q, -p/2 < q < p/2

Now we will see one of the ways an inverse of a trigonometric function can be useful.

Example 3   The designer for an art museum is laying out a room for display of a famous large painting that measures 5 feet high by 12 feet long, and that will be hung with its bottom edge 6 feet from the floor. The preferred viewing place in the room will be a bench to be placed at a distance `A` from the wall. If the average (seated) viewer's eyes are 4 feet above the floor, what should the distance `A` be in order to maximize the viewing angle `theta` (see Figure 12)?

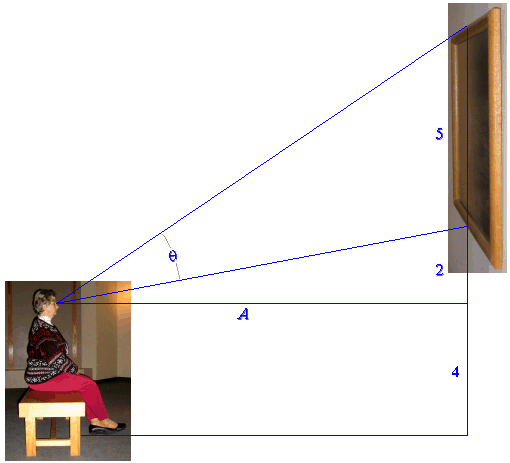
Figure 12   Picture at an exhibition

Solution (partial)   In Figure 13 we have extracted the essential features of Figure 12.

Figure 13   The viewing angle

The distance `A` is one side of a right triangle that is made up of two other triangles. From these two triangles, we see that

`tan text[(]theta + phi text[)]=7/A` and `tan text[(]phi text[)]=2/A`.

If we take inverse tangents of both sides of both equations, we find

`theta+phi=tan^(-1)(7/A)` and `phi=tan^(-1)(2/A)`.

When we subtract the second equation from the first, we get a formula for `theta` as a function of `A`:

`theta=tan^(-1)(7/A)-tan^(-1)(2/A)`.

We show a graph of this function in Figure 14.

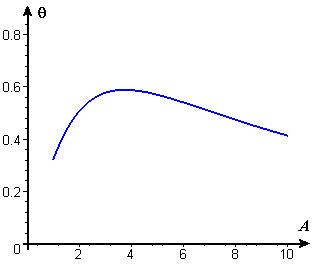
Figure 14   Viewing angle as a function of distance from wall

Not surprisingly, if the bench is either too close to the wall or too far away, the viewing angle is small, and there is a single maximum point at a distance of just under 4 feet. To locate the maximum exactly — which may or may not be important to the designer — we need a formula for the derivative of the inverse tangent (or "arctangent") function so we can find where the derivative takes the value `0`.

In the process of finding the derivative of the arctangent, we use the derivative of the tangent — which we just saw (on the preceding page) is the square of the secant function.

Activity 6

There are two ways to find a formula for the derivative of the arctangent function:

1. Use implicit differentiation and the inverse relationship

   `tan(tan^(-1) x)=x`.

2. Use the formula for differentiation of an inverse function.

Do it both ways, and confirm that both lead to the same formula.

Comment on Activity 6

Solution for Example 3 (continued)   Now that we have a formula for the derivative of the arctangent function, we can complete the calculation of a maximum value for `theta` as a function of `A`:

d ⁢ θ d ⁢ A	= d d A [ tan -1 ( 7 A ) - tan -1 ( 2 A ) ]
	= 1 1 + ( 7 A ) 2 ⁢ d d A 7 A - 1 1 + ( 2 A ) 2 ⁢ d d A 2 A
	= 1 1 + ( 7 A ) 2 ⁢ ( - 7 A 2 ) - 1 1 + ( 2 A ) 2 ⁢ ( - 2 A 2 )
	= - 7 A 2 + 49 + 2 A 2 + 4

This last expression is `0` when `2 A^2+98=7 A^2+28`, that is, when `A^2=14`. The positive solution for `A` is `sqrt(14)`, or about `3.74` (feet), which is in agreement with Figure 14.

Checkpoint 3

Activity 7

Follow the pattern of Activity 6 to find a derivative formula for the arcsine function. You will need to use the relationship between the arcsine and the arccosine, which is illustrated in Figure 15. In the Figure, `y=sin^(-1) x` — read this as "`y` is the angle whose sine is `x`." Then you need to fill in the blank in "`y` is the angle whose cosine is ________." You will see where you need this in the derivative calculation.

Figure 15   `y=sin^(-1) x`

Comment on Activity 7