Chapter 5
Modeling with Differential Equations
5.5 Trigonometric and
Inverse Trigonometric
Functions
Exercises
-
- Calculate the derivative of `sec theta = 1/(cos theta) .`
- Express the answer to part (a) in terms of the functions `sec theta` and `tan theta.`
- Find the second derivative of `sec theta.`
- Use your graphing tool to draw the graph of `sec theta` on the interval from `-2 pi` to `2 pi,` and match the features of the graph with properties of the function as defined in part (a), as well as properties of the first and second derivatives.
- What is the period of `sec theta`? Explain.
- Calculate each of the following derivatives.
- `d/(dt) tan 5t`
- `d/(dx) sin 5x tan 5x`
- `d/(dx) tan^(-1) 5x`
- `d/(dt) cos 5t tan 5t`
- `d/(dt) e^(-t) tan 5t`
- `d/(dx) sin^(-1) 5x tan 5x`
- `d/(dx) e^(-2x) tan^(-1) 5x`
- `d/(dt) sin 5t tan^(-1) 5t`
- Calculate each of the following second derivatives.
You may need the result of Exercise 1, parts (a) and (b).
- `d^2/(dt^2) tan 5t`
- `d^2/(d t^2) sin^(-1) 5t`
- `d^2/(d t^2) tan^(-1) 5t`
- `d^2/(d theta^2) cos 5theta tan 5theta`
-
- Calculate the derivative of the cotangent function, `cot theta = (cos theta)/(sin theta) .`
- Express the answer to part (a) in terms of the cosecant function `csc theta=1/(sin theta) .`
- Use your graphing tool to draw the graph of `cot theta` on the interval from `-2 pi` to `2 pi,` and match the features of the graph with properties of the function as defined in part (a), as well as properties of the derivative.
- What is the period of `cot theta`? Explain.
-
- Calculate the derivative of `csc theta = 1/(sin theta) .`
- Express the answer to part (a) in terms of the functions `csc theta` and `cot theta.`
- Use your graphing tool to draw the graph of `csc theta` on the interval from `-2 pi` to `2 pi,` and match the features of the graph with properties of the function as defined in part (a), as well as properties of the derivative.
- What is the period of `csc theta`? Explain.
- In Example 3, we determined the optimal distance for placing the museum bench to maximize the vertical viewing angle for a picture on the wall. If Figure 12 were redrawn with that optimal distance, it would look more like Figure E1.
- If you were the designer, would you place the bench this close to the wall? Why or why not?
- Figure E2 repeats Figure 14 showing the vertical viewing angle as a function of distance from the wall. What do you see in this figure to suggest that a different placement might be a better design? Explain.
- Figure E3 shows a right triangle in which `y` is the angle whose cosine is `x.` That is, `y=cos^(-1) x.`
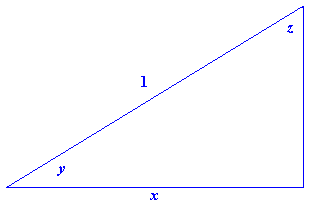
Figure E3 `y=cos^(-1) x`- How is the angle `z` related to `x`?
- Explain why `cos^(-1) x =pi/2-sin^(-1) x.`
- What is the derivative of `cos^(-1) x`? (You should be able to answer this with only mental calculation.)
- What is the domain of the inverse cosine function? What is its range?
- Use your graphing tool to graph both arcsine and arccosine.
- What do you think we meant in the Section Summary (preceding page) when we said the inverse cosine "is less interesting and less useful than the inverse sine"?
-
- What is the domain of the inverse tangent function? What is its range?
- Use your graphing tool to graph the arctangent function.
- Use your graphing tool to graph the derivative of the arctangent function.
- What is the steepest slope on the graph of the arctangent function, and where does it occur?
- Figure E4 shows a right triangle in which `y` is the angle whose secant is `x.` That is, `y=sec^(-1) x.`
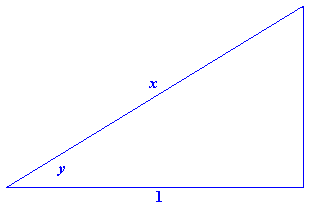
Figure E4 `y=sec^(-1) x`- What is the tangent of the angle `y`?
- Use implicit differentiation and the result of Exercise 1(a) to find `dytext[/]dx`. You will need the answer to part (a) to write the result as a function of `x.`
- What is the domain of the secant function? What is its range?
- Use your graphing tool to graph both secant and its derivative. Match features of the two graphs.
- Figure E5 shows a right triangle in which `y` is the angle whose cosecant is `x.` That is, `y=csc^(-1) x.`
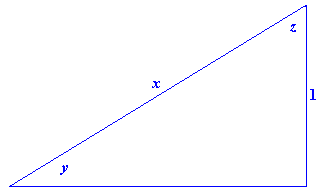
Figure E5 `y=csc^(-1) x`- How is the angle `z` related to `x`?
- Explain why `csc^(-1) x =pi/2-sec^(-1) x.`
- What is the derivative of `csc^(-1) x`? (After doing Exercise 10, you should be able to answer this with only mental calculation.)
- What is the domain of the inverse cosecant function? What is its range?
- Use your graphing tool to graph both arcsecant and arccosecant.
 |
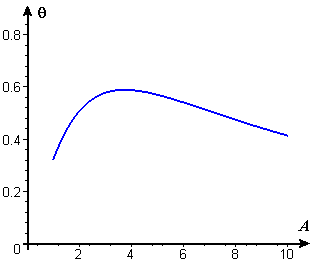 |
Figure E1 Optimal viewing angle |
Figure E2 Viewing angle vs. distance |

