Exercises

1. Calculate each of the following derivatives.

   `d/(dt) e^(-t) sin 5t`	`d/(dx) x^2 3^x`
   `d/(dx) e^(-2x) cos 5x`	`d/(dt) cos^3 2t`
   `d/(dx) text[(] ln x^2text[)] cos 2x`	`d/(dt) cos text[(] 2t^3text[)]`
   `d/(dt) 3^(2t)`	`d/(dx) sin^(-1) x tan 2x`
   `d/(dx) e^(2x)/(sin 5x)`	`d/(dx) sin^(-1) x tan^(-1) 2x`

2. Calculate each of the following second derivatives.

   `d^2/(dt^2) e^(-t) sin 5t`	`d^2/(dx^2)  x^2 3^x`
   `d^2/(d theta^2) e^(-2theta) cos 5theta`	`d^2/(dt^2)  cos^3 2t`
   `d^2/(d theta^2) text[(] ln theta^2text[)] cos 2theta`	`d^2/(dt^2)  cos text[(] 2t^3text[)]`
   `d^2/(d theta^2) 3^(2theta)`	`d^2/(dx^2)  tan 2x`
   `d^2/(dx^2) e^(2x)/(sin 5x)`	`d^2/(dx^2)  tan^(-1) 2x`

3. Find the derivative of each of the following functions.

   `z=7 ln text[(] 3+2t text[)]`	`z=1/(2t+1)`
   `y=x^6+4x^2+6x^(-2)`	`z=7/(3+2t)`
   `y=2 e^(5x)`	`y=(sin 2u)/(cos 5u)`
   `y=text[(] sin 2t text[) (] cos 5t text[)]`	`z=text[(] 2t+1text[)]^12`
   `y=text[(] sin^(-1) 2t text[) (] cos 5t text[)]`	`u=tan^3 2x`

4. For each of the following functions,
   1. graph the function,
   2. graph the derivative from your calculation in Exercise 3, and
   3. explain how appropriate properties of the derivative graph confirm your symbolic calculation.

   `z=7 ln text[(] 3+2t text[)]`	`z=1/(2t+1)`
   `y=x^6+4x^2+6x^(-2)`	`z=7/(3+2t)`
   `y=2 e^(5x)`	`y=(sin 2u)/(cos 5u)`
   `y=text[(] sin 2t text[) (] cos 5t text[)]`	`z=text[(] 2t+1text[)]^12`
   `y=text[(] sin^(-1) 2t text[) (] cos 5t text[)]`	`u=tan^3 2x`

5. Find the derivative of each of the following functions.

   `y=3 sin t cos 3t`	`z=1/(text[(]2t+1text[)]^2)`
   `u=cos^2 3t`	`z=7/(text[(]3+2t text[)]^3)`
   `v=cos text[(]3t^2text[)]`	`y=x^7+3x^2+6`
   `y=sin 2t-cos 5t`	`z=2^(5x)`
   `y=tan 2t-cos 5t`	`v=sin^(-1) 5y`

6. For each of the following functions,
   1. graph the function,
   2. graph the derivative from your calculation in Exercise 5, and
   3. explain how appropriate properties of the derivative graph confirm your symbolic calculation.

   `y=3 sin t cos 3t`	`z=1/(text[(]2t+1text[)]^2)`
   `u=cos^2 3t`	`z=7/(text[(]3+2t text[)]^3)`
   `v=cos text[(]3t^2text[)]`	`y=x^7+3x^2+6`
   `y=sin 2t-cos 5t`	`z=2^(5x)`
   `y=tan 2t-cos 5t`	`v=sin^(-1) 5y`

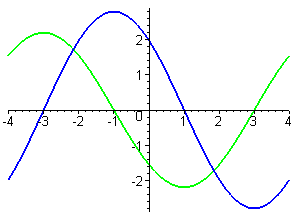
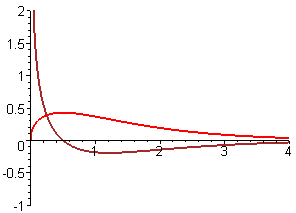
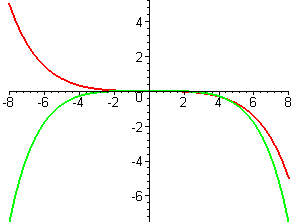
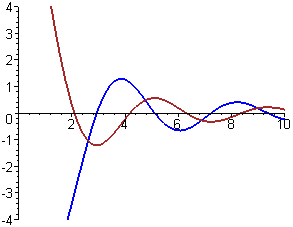
7. In each part of this exercise, graphs of two functions are shown. In each case, one of the functions is the derivative of the other. Decide which function is `f` and which is `f'`. Give as many reasons as you can for your choice.
   1. 
   
   
   2. 
   
   
   3. 
   
   
   4.