Here, again, is the logistic growth differential equation we proposed in the preceding section to solve:

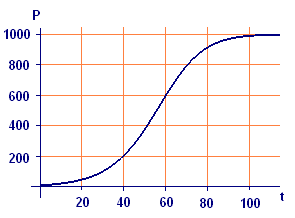
where `k` and `M` are constants. The graphs of the solutions are called logistic curves. You saw one in Figure 1 in Section 6.2, which we repeat here, and you drew several yourself in Activity 3 in the preceding section.

6.3.1  A New Antidifferentiation Problem

We begin the solution process just as we did for the natural-growth equation, by separating the variables:

Now we want to antidifferentiate both sides. When we do that we will have rewritten the problem as

An antidifferential of `(dP)/(Ptext[(]M-Ptext[)])=` some antidifferential of `k dt`.

This presents us with a new problem: The antidifferentiation on the right is easy — and just like the natural-growth case — but the one on the left is different from anything we have seen before.

Our immediate problem is not a population problem, or even a differential equation problem. The question we have to answer is, "What function of `P` has differential `(dP)/(Ptext[(]M-Ptext[)])`?" That's the same as asking what function has derivative `1/(Ptext[(]M-Ptext[)])`. And we don't have a ready answer, because nothing like this has turned up yet in our derivative formulas.

To emphasize the fact that the question in the last paragraph is unrelated to population growth — and because we might want to use the answer in some other context later — let's reformulate the question as

"What function of a variable `x` has derivative `1/(xtext[(]c-x text[)])`?"

You may think of `x` as representing `P` and `c` as representing `M` if you wish.

We want to rewrite this problem in a form we can deal with more easily, i.e., use algebra to transform the problem into one where we can recognize what to do. The question we need to ask is: "What kind of algebraic calculation could have produced

`1/(xtext[(]c-x text[)])`?"

This is a little like playing the TV quiz game Jeopardy!:

"The answer is `1/(xtext[(]c-x text[)])`; what is the question?"

Activity 1

Write down your own thoughts about this question. You may think of more than one way to answer the question. That's good, because we may need more than one way.