6.3.5 Population Growth in the United States

Is the logistic model of any real interest? Sure, some biologists might be interested in fruit flies, but are there any other populations that actually behave that way?

We began Chapter 2 with Thomas Malthus's observation, written about 1800, of the inevitable dire consequences of natural (exponential) growth of the human population of the earth. Some years later, the Belgian mathematician P. F. Verhulst modified Malthus's prediction with the observation that the (human) population of any given region — including the whole Earth — could not exceed some "maximum capacity" for that region. He may have been the first to propose the logistic equation

as a model for constrained natural growth, and he definitely had human populations in mind.

However, Verhulst was unable to test his theory or to compare it with Malthus's for two reasons:

1. In his day, there were no reliable estimates of world population at any time, past or present, so he had no way of estimating `k`, or `P_0`, or `M`.
2. Even if he knew, or could guess, reasonable values for the parameters, his formula for population would have to give essentially the same results as an exponential formula, since the population was clearly still very small relative to `M`.

Frustrated by his inability to say anything meaningful about world population — other than to suggest a reason why Malthus might be wrong — Verhulst turned to the only available source of good information about some large population: the U.S. Census. By 1840, there were six censuses, the results of which are shown in Table 1. Verhulst used these data to make a prediction, based on the logistic model, of the U.S. population years 100 later; he was off by only 1%. He didn't live to see how his prediction worked out, of course, so he probably died frustrated. His accomplishment was remarkable — perhaps also a bit lucky — because it took into account nothing but natural biological reproduction and the existence of some unknown maximum population — nothing about immigration, wars, depression, or anything else that affected our population in either direction over that 100-year period.

On the next page we will explore a technique for determining whether data might come from a logistic curve and, if so, determining the parameters in the formula for that curve. To give you some feel for Verhulst's remarkable prediction, we show in Figure 2 a plot of the actual census data from 1790 to 1840, along with exponential and logistic projections from those six data points.

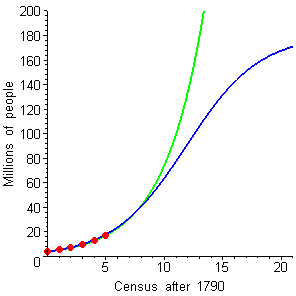
Figure 2  Verhulst's data and possible projections,
exponential (green) and logistic (blue)