Exercises

1. Sketch by hand the solution of each of the following initial value problems. You do not need to solve the problems — just show the essential features of the solutions.

   `(dP)/(dt)=2Ptext[(]4-Ptext[)], Ptext[(]0text[)]=1`	`(dP)/(dt)=2Ptext[(]4-Ptext[)], Ptext[(]0text[)]=4`
   `(dP)/(dt)=2Ptext[(]4-Ptext[)], Ptext[(]0text[)]=3`	`(dP)/(dt)=2Ptext[(]4-Ptext[)], Ptext[(]0text[)]=5`

2. For each of the following relations, find numbers `A` and `B` so that the relation holds for all appropriate values of `x`.

   `A/x+B/(5-x)=1/(xtext[(]5-xtext[)])`	`A/x+B/(x+4)=1/(3xtext[(]x+4text[)])`
   `A/x+B/(5+x)=1/(xtext[(]5+xtext[)])`	`A/x+B/(x-4)=1/(3xtext[(]4-xtext[)])`
   `A/(2+x)+B/(2-x)=1/(4-x^2)`	`A/(3-2x)+B/(3+2x)=1/(9-4x^2)`

3. Find an antiderivative for each of the following functions.

   `1/(xtext[(]5-xtext[)])` for `0<x<5`	`1/(3xtext[(]x+4text[)])` for `x>0`
   `1/(xtext[(]5+xtext[)])` for `x>0`	`1/(3xtext[(]4-xtext[)])` for `0<x<4`
   `1/(4-x^2)` for `-2<x<2`	`1/(9-4x^2)` for `-3/2<x<3/2`

4. In Activity 3 you showed that

   an antidifferential of `(dx)/(xtext[(]c-xtext[)])=1/c ln x-1/c lntext[(]c-xtext[)]`

   when `x` is restricted to range between `0` and `c`. Show that the restriction on the range of `x` can be dropped — that is, we can allow `x` to be negative or greater than `c` — if we write the formula as

   an antidifferential of `(dx)/(xtext[(]c-xtext[)])=1/c ln |x|-1/c ln|c-x|`.

5. Use the preceding exercise to show that
   1. `ln (x/(x-1))` is an antiderivative for `1/(xtext[(]1-xtext[)])` for `x>1`.
   2. `ln ((-x)/(x-1))` is an antiderivative for `1/(xtext[(]1-xtext[)])` for `x<0`.
6. Find an antiderivative for each of the following functions for the indicated domain.

   `1/(xtext[(]5-xtext[)])` for `x<0`	`1/(3xtext[(]x+4text[)])` for `-4<x<0`
   `1/(xtext[(]5+xtext[)])` for `-5<x<0`	`1/(3xtext[(]4-xtext[)])` for `0<x<4`
   `1/(4-x^2)` for `x>2`	`1/(9-4x^2)` for `x<-3//2`

7. Find an antiderivative for each of the following functions for the indicated domain.

   `1/(xtext[(]5-xtext[)])` for `x>5`	`1/(3xtext[(]x+4text[)])` for `x<-4`
   `1/(xtext[(]5+xtext[)])` for `x<-5`	`1/(3xtext[(]4-xtext[)])` for `0<x<4`
   `1/(4-x^2)` for `x<-2`	`1/(9-4x^2)` for `x>3//2`

8. In case you didn't do Exercise 9 in Section 4.5 (or don't remember how it went), we repeat a version of it here for your convenience. We start with the logistic growth equation,

   `(dP)/(dt)=kPtext[(]M-P text[)]`,

   where `Ptext[(]t text[)]` is the population at time `t`, `M` is the maximum supportable population of the environment, and `k` is a proportionality constant.
   1. Explain why the population must be growing most rapidly at a time at which the second derivative of `P` is zero.
   2. Differentiate both sides of the differential equation to find an expression for the second derivative. (The Product Rule works for differentiating the right-hand side, but you can make the computation easier if you rewrite the expression in another form first.) Be careful with your differentiation — you are differentiating with respect to `t`, not `P`, so the Chain Rule must come into play every time you run into the unknown function `P`.
   3. What does your expression for the second derivative tell you about the population size when the growth rate is maximal?
   4. How does this lead to our estimate for `M` in the U.S. Population Example?
9. Figure E2 (repeated here from Section 6.2) makes it clear that the logistic growth model is biologically meaningful even if `P_0` is greater than `M`. This might be the case if there were a sudden wave of immigration — for example, large numbers of refugees from a civil war in a neighboring country — or an overstocking of a wildlife refuge, or a concentration of wildlife in a habitat that is shrinking because of development. Find the general solution of the logistic growth model when `P_0` is greater than `M`. (Hint: Review Exercise 4.)

   

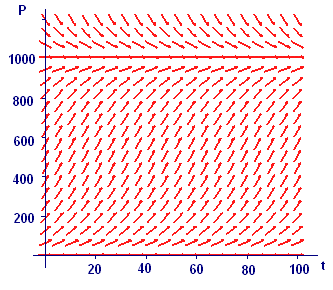   Figure E2   Slope field for `(dP)/(dt)=0.00009P text[(]1000-P text[)]`
10. The logistic initial value problem,

    `(dP)/(dt)=kPtext[(]M-P text[)],   Ptext[(]0text[)]=P_0,`

    is mathematically meaningful for every starting point — negative, zero, less than `M`, equal to `M`, and greater than `M`. Expand on the preceding exercise to find the general solution in every case.
11. You may have noticed that we never checked our solution of the logistic growth equation. We leave this to you, with the warning that this is a serious challenge to your algebraic skills. You will find it easiest to work with the form

    `P=(P_0 M)/(text[(]M-P text[)]e^(-Mkt)+P_0`.

    First do the easy part: Check that `P=P_0` when `t=0`. Then verify that the function `Ptext[(]t text[)]` satisfies the growth equation

    `(dP)/(dt)=kPtext[(]M-P text[)]`.

    [Hint: Calculate `dP`/`dt` and `kPtext[(]M-P text[)]` separately. Then simplify each until you can see that the two expressions are the same.]