7.1.6 The Definite Integral

We repeat part of the last paragraph on the preceding page describing the relationship between velocity and area:

The total distance traveled by an object moving with speed `vtext[(]t text[)]` from time `t=a` to time `t=b` is the limiting value (as `n` becomes large) of the sums

where `Delta t = (b-a)/n` and `t_k=a+k Delta t` for `k=0, 1, ... , n`.

This subdivide-and-conquer calculation, which computes distance from velocity and area under the graph of a function, also occurs in many other applications. Thus it is useful to have a notation to summarize it so we don't have to keep repeating the description just given.

Definition   If `ftext[(]t text[)]` is a continuous function defined on the interval `a ≤ t ≤ b`, then the definite integral of `f` from `a` to `b` is the number to which the sums ${\displaystyle \sum _{k=1}^{n}f\left(t_{k-1}\right)\Delta t}$ converge as `n` becomes large. Here `Delta t = text[(]b-a text[)]`/`n` and `t_k=a+k Delta t` for `k=0,1, ... n`.

Notation   We use the symbol ${\displaystyle {\int }_a^{b}f\left(t\right)dt}$ to stand for the definite integral of `f` from `a` to `b`.

Our definition of the definite integral uses the phrase "continuous function," which we have used informally on many previous occasions. This concept is an abstraction of the idea of "continuously varying quantity," such as temperature. The technical definition of "continuous" is a little complicated and would interfere with our development of integral calculus without adding much to our understanding at this point. In the next subsection we illustrate the meaning of this word by giving examples of familiar continuous functions.

A dictionary definition of the verb "integrate" is "to make into a whole by bringing all parts together." That's a pretty good description of what we are doing when we chop a computational problem into tiny parts, evaluate each part, and then add the results. The adjective "definite" refers to the appearance of definite endpoints of the interval being subdivided. These endpoints appear in both the computational description and the notation. Often the adjective is dropped, and we speak of the integral of a function over an interval. However, we will soon introduce the phrase "indefinite integral" for an entirely different concept, and then we will need the adjectives to distinguish the two concepts.

How do we make sense of the notation? Compare the symbols

There is a definite correspondence: The integral sign `∫` — an elongated S standing for sum — corresponds to the sigma notation for the sum on the right. The endpoints `a` and `b` correspond to the first and last values of the summation index `k`, because `a=t_0` and `b=t_n`. The function values `ftext[(]t text[)]` at every value of `t` between `a` and `b` correspond to the values `ftext[(]t_k text[)]` at equally spaced values of `t` in the sum. And the differential `dt` — so far, just part of the notation — corresponds to the difference `Delta t`. The effect of this notation is to suggest the idea of summing infinitely many products of the form `ftext[(]t text[)] dt`, each of which is infinitely small because of the infinitesimal factor `dt`. If you remember that this really means the result of a limiting process in which the number `n` of terms in the sum becomes arbitrarily large, then you will have a sensible meaning for the apparently nonsensical phrase "summing infinitely many infinitely small products." And the integral notation will serve as a constant reminder of the complicated process by which we defined the definite integral — the process by which we bring all the parts together.

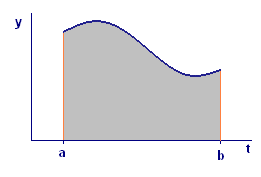
Finally, our transformation of the distance problem into an area problem provides us with a visual image of the definite integral (Figure 7): If `ftext[(]t text[)]` is nonnegative for all values of `t`, then ${\int }_a^{b}f\left(t\right)dt$ represents the area of the region in the `text[(]t,y text[)]`-plane bounded below by the `t`-axis, bounded on the sides by the lines `t=a` and `t=b`, and bounded above by the curve `y=ftext[(]t text[)]`.