7.1.7 Continuous Functions

As promised on the preceding page, we now take up the concept of continuous function. Instead of giving a formal definition, we give some examples of continuous functions. These examples will reassure you that any function you are likely to see as a candidate for integration is, in fact, continuous. They will also emphasize — again — the importance of paying attention to the domain of a function, not just to its rule.

First, all locally linear functions are continuous. That is, if a function has a derivative at every point of its domain, it is a continuous function. Since most of our formula-based functions are locally linear, you should be reassured already.

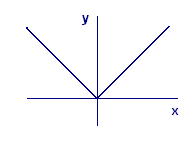
Second, there are some familiar functions that are not locally linear (at certain points) but that are nevertheless continuous. For example, the absolute value function, `ftext[(]x text[)]=|x|`, is one of these (see Figure 8). There is a sharp point on its graph at `text[(]0,0 text[)]`, but there is no break or jump in the graph at that point. This is one way to think of what it means to be continuous: no breaks or jumps in the graph.

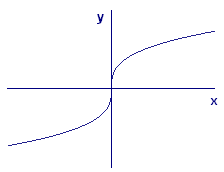
Third, there are some familiar functions whose graphs don't have corners or sharp points but that fail to have derivatives at certain points. For example, consider `gtext[(]x text[)]=x^(1//3)` (Figure 9). The derivative of this function (Figure 10) is `g' text[(]x text[)] = text[(]1text[/]3text[)]x^(-2//3)`, which fails to have a value at `x=0`. In fact, the graph of `g` is vertical at `x=0`, so its tangent line at `text[(]0,0 text[)]` can't have a slope. But again, there is no break or gap, and `g` is continuous.

Figure 9   Graph of `gtext[(]x text[)]=x^(1//3)`	Figure 10   Graph of `g'text[(]x text[)]=text[(]1text[/]3text[)]x^(-2//3)`

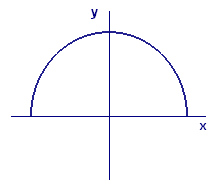
Similarly, the function `htext[(]x text[)]=sqrt(1-x^2)` has a graph that is a semicircle of radius `1` on the domain `[-1,1]` (see Figure 11). At the endpoints of the domain, the tangent lines are vertical and hence have no slope — but the function is nevertheless continuous on its entire domain.

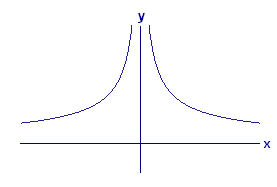
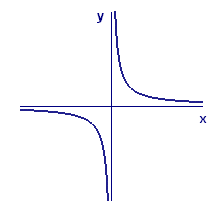
Fourth, and less intuitive, the function `qtext[(]x text[)]=1//x` is continuous on its domain, even though its graph has a rather large gap in the middle (see Figure 12). The point is that `0` is not in the domain of this function. We can integrate this function between numbers `a` and `b`, but only if the interval `[a,b]` does not contain `0`. That is, `a` and `b` must both be positive or both be negative. On such intervals, the reciprocal function has no breaks or jumps. Similarly, any rational function (i.e., quotient of polynomial functions) is continuous, but only on intervals entirely contained in its domain.

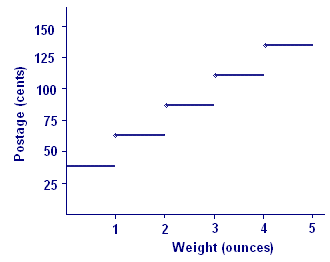
What functions are not continuous? A simple example is the first-class postage function (Figure 13), which has a value for every positive weight (up to the maximum weight) but which also has obvious jumps at whole numbers of ounces. Similarly, the approximate speed function represented by Table 1 — for which we assumed constant speeds for one-minute time intervals — also has jumps at whole numbers of minutes. It would be easy enough to define a definite integral for these step functions — just add up rectangular areas. We chose not to include that idea in our definition of the integral because it would complicate the definition without adding any benefit.

The bottom line is that you are unlikely to encounter a formula-based function `f` for which ${\int }_a^{b}f\left(t\right)dt$ is not already defined — or could be — as long as you make sure the interval `[a,b]` is contained in the domain of `f`.

Checkpoint 3