Exercises

1. Use the Fundamental Theorem of Calculus to evaluate each of the following definite integrals.

   `int_1^3 t^3 dt`	`int_(-3)^0 t^3 dt`	`int_(-1)^3 t^3 dt`
   `int_1^3 t^4 dt`	`int_(-3)^0 t^4 dt`	`int_(-1)^3 t^4 dt`
   `int_0^(pi//2) cos t dt`	`int_0^(pi//2) 5 cos t dt`	`int_0^(pi//2) sin  t dt`
   `int_0^(pi//2) 5 sin t dt`	`int_1^3 1/t  dt`	`int_2^4 1/t  dt`
   `int_2^4 1/(t+1) dt`	`int_3^5 1/(t+1) dt`	`int_0^1 e^t dt`
   `int_(-1)^1 e^t dt`	`int_0^1 e^(-t) dt`	`int_0^(-1) e^(-t) dt`

2. For each of the following definite integrals,
   1. use the integral key on your calculator (or integral command in your computer algebra system) to evaluate the integral,
   2. graph the function being integrated on the indicated interval, and
   3. interpret the value of the integral in terms of area.

   `int_1^3 t^3 dt`	`int_(-3)^0 t^3 dt`	`int_(-1)^3 t^3 dt`
   `int_1^3 t^4 dt`	`int_(-3)^0 t^4 dt`	`int_(-1)^3 t^4 dt`
   `int_0^(pi//2) cos t dt`	`int_0^(pi//2) 5 cos t dt`	`int_0^(pi//2) sin  t dt`
   `int_0^(pi//2) 5 sin t dt`	`int_1^3 1/t  dt`	`int_2^4 1/t  dt`
   `int_2^4 1/(t+1) dt`	`int_3^5 1/(t+1) dt`	`int_0^1 e^t dt`
   `int_(-1)^1 e^t dt`	`int_0^1 e^(-t) dt`	`int_0^(-1) e^(-t) dt`

3. Find the average value of each of the following functions on the indicated interval.

   `t^3` on `[1,3]`	`t^3` on `[-3,0]`	`t^3` on `[-1,3]`
   `t^4` on `[1,3]`	`t^4` on `[-3,0]`	`t^4` on `[-1,3]`
   `cos t` on `[0,pi/2]`	`5 cos t` on `[0,pi/2]`	`sin t` on `[0,pi/2]`
   `5 sin t` on `[0,pi/2]`	`1/t` on `[1,3]`	`1/t` on `[2,4]`
   `1/(t+1)` on `[2,4]`	`1/(t+1)` on `[3,5]`	`e^t` on `[0,1]`
   `e^t` on `[-1,1]`	`e^(-t)` on `[0,1]`	`e^(-t)` on `[-1,1]`

4. Find the average value of each of the following functions on the interval `[-1,1]`, and explain why these calculations are so easy.

   a.  `ftext[(]x text[)]=x`

   b.  `gtext[(]x text[)]=x^3-x`

   c.  `htext[(]x text[)]=sin x`

5. Evaluate each of the following indefinite integrals.

   `int  t^4 dt`	`int  t^5 dt`	`int  (t+1)^5 dt`
   `int  sin t dt`	`int  sin 2t dt`	`int  cos t dt`
   `int  cos 2t dt`	`int  e^t dt`	`int  3 e^t  dt`
   `int  e^(3t) dt`	`int  1/t  dt`	`int  1/(t+1) dt`
   `int  sqrt(t) dt`	`int` `1/sqrt(t) dt`	`int`  `t^(1/3) dt`

6. Use the Fundamental Theorem of Calculus to evaluate each of the following definite integrals. Practice using the notation of the indefinite integral as an intermediate step. Check your answers with the integral key on your calculator or the integral command in your computer algebra system. Note that if an answer does not check, the likely place to look for an error is in your calculation of the indefinite integral.

   `int_(-1)^1  t^4 dt`	`int_(-1)^1  t^5 dt`	`int_(-1)^1  (t+1)^5 dt`
   `int_0^pi  sin t dt`	`int_0^pi  sin 2t dt`	`int_0^(pi//4)  cos t dt`
   `int_0^(pi//4)  cos 2t dt`	`int_-1^2  e^t dt`	`int_-1^2  3 e^t  dt`
   `int_-1^2  e^(3t) dt`	`int_1^4  1/t  dt`	`int_1^4  1/(t+1) dt`
   `int_1^3  sqrt(t) dt`	`int_1^3  1/sqrt(t) dt`	`int_1^3  t^(1/3) dt`

7. Find the average value of each of the following functions on the indicated interval.

   ` t^4` on `[-1,1]`	` t^5` on `[-1,1]`	` (t+1)^5` on `[-1,1]`
   `sin t` on `[0,pi]`	`sin 2t` on `[0,pi]`	`cos t` on `[0,pi/4]`
   `cos 2t` on `[0,pi/4]`	`e^t` on `[-1,2]`	`3 e^t` on `[-1,2]`
   `e^(3t)` on `[-1,2]`	`1/t` on `[1,4]`	`1/(t+1)` on `[1,4]`
   `sqrt(t)` on `[1,3]`	`1/sqrt(t)` on `[1,3]`	`t^(1/3)` on `[1,3]`

8. Each of the following integrals defines a function `f` of `x`. Use your graphing tool to graph each of these functions.

   `int_0^x e^(t^2) dt`	`int_1^x e^(t^2) dt`	`int_(-1)^x e^(t^2) dt`
   `int_0^x t sin(t^3) dt`	`int_1^x t cos(t^3) dt`	`int_(-1)^x sqrt(1+t^2) dt`

9. Each of the following integrals defines a function `f` of `x`. In each case, find `d/(dx) ftext[(]x text[)]`.

   `int_0^x e^(t^2) dt`	`int_1^x e^(t^2) dt`	`int_(-1)^x e^(t^2) dt`
   `int_0^x t sin(t^3) dt`	`int_1^x t cos(t^3) dt`	`int_(-1)^x sqrt(1+t^2) dt`

10. Evaluate each of the following indefinite integrals.

    `int``(x^(2//3)-x^(1//3)) dx`	`int``(x^(4//3)+x^(5//3)) dx`
    `int``(x^(1//2)-x^(3//2)) dx	`int  x^7 dx`
    `int  sin 3x dx`	`int  (1+3x-x^2) dx`
    `int  (1+x^2)^2 dx`	`int  e^(-5x) dx`

11. Evaluate each of the following definite integrals. Use your computer or calculator to check your results.

    `int_0^2  (x^(2//3)-x^(1//3)) dx`	`int_1^2  (x^(4//3)+x^(5//3)) dx`
    `int_0^1  (x^(1//2)-x^(3//2)) dx	`int_5^11  x^7 dx`
    `int_0^pi  sin 3x dx`	`int_(-1)^3  (1+3x-x^2) dx`
    `int_(-2)^2  (1+x^2)^2 dx`	`int_(-1)^1  e^(-5x) dx`

12. Estimate each of the following definite integrals.

    `int_0^(pi//2)  sin^2 x dx`

    `int_0^(pi//2)  cos^2 x dx`

    `int_0^1 1/(1+x^2) dx`

13. 1. Use your graphing tool to sketch the graph of `ftext[(]t text[)]=sqrt(1+t^2)`.
    2. Use your graphing tool and an exact formula (not Euler's Method) to sketch the solution of the initial value problem `(dy)/(dt)=sqrt(1+t^2)` with `ytext[(]0 text[)]=0`.
    3. Make a sketch on paper of the solution of `(dy)/(dt)=sqrt(1+t^2)` with `ytext[(]0 text[)]=2`.
14. 1. Use your graphing tool to sketch the graph of `ftext[(]t text[)]=sin(t^2)`.
    2. Use your graphing tool and an exact formula (not Euler's Method) to sketch the solution of the initial value problem `(dy)/(dt)=sin(t^2)` with `ytext[(]0 text[)]=0`.

    Figure E1   Which is
    the antiderivative?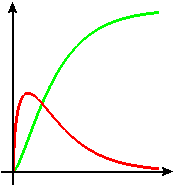

    3. Make a sketch on paper of the solution of `(dy)/(dt)=sin(t^2)` with `ytext[(]0 text[)]=2`.

 

15. Figure E1 shows the graphs of two functions we will call `f` and `g`. The function `g` is an antiderivative of `f`.

    1. Which graph is that of `f` and which is that of `g`?
    2. Write down a formula that defines `g` in terms of `f`.

 

16. Figure E2 shows the graph of a function `f` on the interval `[0,2]`. We define two more functions, `Ftext[(]x text[)]` and `gtext[(]x text[)]` on the same interval:

    Figure E2   Graph of `ftext[(]x text[)]`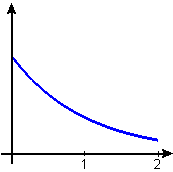

    `Ftext[(]x text[)]=int_0^x ftext[(]t text[)] dt`   for `0<=x<=2`,

    and

    `gtext[(]x text[)]=int_0^x f'text[(]t text[)] dt`   for `0<=x<=2`.

    With the information given, respond as precisely as you can to each of the following:

    1. Complete the sentence: The value of `F` at `1` is  ________.
    2. Complete the sentence: The value of `F'` at `1` is ________.
    3. Complete the sentence: The value of `g` at `1` is  ________.
    4. Complete the sentence: The value of `g'` at `1` is ________.
    5. Sketch the graph of `F`.
    6. Sketch the graph of `g`.

Figure E3   What is the average slope?

 

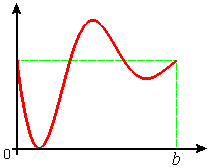
17. Figure E3 shows the graph of a locally linear function `ftext[(]x text[)]` on the interval `[0,b]` with the property that `ftext[(]0 text[)]=ftext[(]b text[)]`. What is the average value of the derivative `f'text[(]x text[)]` on `[0,b]?` Explain.

 

 

18. Let `s` be the function defined by

    `stext[(]x text[)]=int_0^x e^(-t^2//2)  dt`.

    If `w` is the function defined by `wtext[(]x text[)]=s(x^2)`, show that `w'text[(]x text[)]=2xe^(-x^4//2)`. (Hint: Use the Chain Rule.)

19. Find a function `ftext[(]x text[)]` that satisfies the functional equation

    `ftext[(]x text[)]^2=int_0^x ftext[(]t text[)] dt+1`.

    Is there more than one such function?
Problem contributed by Michael Reed, Duke University.
20. Four calculus students disagree as to the value of the integral `int_0^pi sin^8 x dx`. Jack says it is equal to `pi`. Joan says it is equal to `(35pi)/128`. Ed claims it is equal to `(3pi)/90-1`, while Lesley says it is equal to `pi/2`. One of them is right — which one? (You have no way yet to evaluate the integral exactly — try to eliminate the three wrong answers. If you get stuck, try using a numerical estimate of the integral.)
Problem adapted from Calculus Problems for a New Century, edited by R. Fraga, MAA Notes, No. 28, 1993 .
21. The cost of digging a tunnel is the product of the length of the tunnel and the cost per unit length. If the cost per unit length is a constant, it is easy to calculate the cost of the tunnel. However, the cost per unit length increases as the tunnel gets longer because of the expense of carrying workers and tools in and carrying dirt and rock out. Assume that the dollar cost per foot varies as in Table E1.

    Table E1   Cost per foot for digging a tunnel

    Length (feet)	Cost (`\$` per foot)		Length (feet)	Cost (`\$` per foot)
    0-100	2500		500-600	12500
    100-200	4100		600-700	15100
    200-300	5540		700-800	17900
    300-400	7540		800-900	20900
    400-500	10100		900-1000	24100

    1. Find the total cost for digging a tunnel 1000 feet long.
    2. How much could be saved by starting the 1000-foot tunnel from both ends and making the two halves meet in the middle?
    3. If the half-tunnels of part (b) don't meet in the middle, what can you do, and how much will it cost?
Problem adapted from Calculus Problems for a New Century, edited by R. Fraga, MAA Notes, No. 28, 1993 .
22. Explain the following equalities geometrically.
    1. `int_0^1 x^n dx+int_0^1 x^(1//n) dx=1` for any positive integer `n`.
    2. `int_1^e ln x dx + int_0^1 e^x dx=e`.
Problem adapted from Calculus Problems for a New Century, edited by R. Fraga, MAA Notes, No. 28, 1993 .
23. 1. Find the average value of `x` over the interval `[0,1]`; of `x^2`; of `x^3`.
    2. Find the average value of `x^n` over the interval `[0,1]`, where `n` is any integer `>=1`.
    3. What happens to the average value of `x^n` over the interval `[0,1]` as `n` gets larger and larger? Can you explain this?
24. 1. Find the average value of `x` over the interval `[0,1]`; of `x^(1//2)`; of `x^(1//3)`.
    2. Find the average value of `x^(1//n)` over the interval `[0,1]`, where `n` is any integer `>=1`.
    3. What happens to the average value of `x^(1//n)` over the interval `[0,1]` as `n` gets larger and larger? Can you explain this?
25. For each of the following expressions,
    1. sketch a region whose area equals the given expression, and
    2. calculate the area of the region.
    
    
    1. `int_0^(2pi)(sin x+2) dx`
    2. `int_0^2x^2 dx+int_2^6(6-x) dx`
    3. `int_-1^2 4 dt-int_-1^2 t^2 dt`
Problem adapted from Unit 7 of Workshop Calculus, by Nancy Baxter, Dickinson College, 1994.

26. Figure E4   Graph of a
    function `y=ftext[(]t text[)]`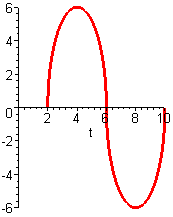

    Figure E4 shows the graph of a function `y=ftext[(]t text[)]`. For each of the following statements,

    1. determine whether the given statement is true or false, and
    2. carefully explain your answer to part (i).

    
    

    1. `int_2^6 ftext[(]t text[)] dt~~-int_6^10 ftext[(]t text[)] dt`
    2. `int_2^6 ftext[(]t text[)] dt+int_6^10 ftext[(]t text[)] dt=int_2^10 ftext[(]t text[)] dt`
    3. `int_2^6 ftext[(]t text[)] dt<24`
    4. `int_4^6 ftext[(]t text[)] dt>0.5[ftext[(]4.5 text[)]+ftext[(]5.0 text[)]+ftext[(]5.5 text[)]+ftext[(]6.0 text[)]]`
Problem adapted from Unit 7 of Workshop Calculus, by Nancy Baxter, Dickinson College, 1994.