Chapter 9
Probability and Integration





9.2 Improper Integrals

9.2.4 More Improper Integrals

Just as we can integrate to `oo`, we can integrate to `-oo` and, for some functions, even from `-oo` to `oo`.

Definitions   If `g text[(] t text[)]` is a continuous function for `t ≤ a`, then the improper integral
∫ - ∞ a g ( t )   d t = lim T → - ∞ ∫ T a g ( t )   d t .

If the limiting value exists as a finite number, we say the improper integral converges. Otherwise, it diverges.

If `g text[(] t text[)]` is a continuous function for all `t` then the improper integral

∫ - ∞ ∞ g ( t )   d t = ∫ - ∞ 0 g ( t )   d t + ∫ 0 ∞ g ( t )   d t .

If both integrals on the right converge, we say the improper integral on the left converges. Otherwise, it diverges.

Example 5

Show that the area under the graph of `y = 1/(1 + t^2)` is `pi` (see Figure 3).

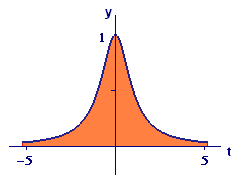
Figure 3   Area under the graph of `y = 1/(1 + t^2)`

Solution   The shaded area is

∫ - ∞ ∞ 1 1 + t 2   d t = ∫ - ∞ 0 1 1 + t 2   d t + ∫ 0 ∞ 1 1 + t 2   d t end solution
  = lim T → - ∞ ∫ T 0 1 1 + t 2   d t + lim U → ∞ ∫ 0 U 1 1 + t 2   d t
  = lim T → - ∞ ⁢   arctan ⁢   t | T 0 + lim U → ∞ ⁢   arctan ⁢   t | 0 u
  = lim T → - ∞ ⁢   ( 0 - arctan ⁢   T ) + lim U → ∞ ⁢   ( arctan ⁢   U - 0 )
  = π 2 + π 2 = π .

The choice of `t = 0` as a dividing point between the left-hand and right-hand improper integrals is merely a matter of convenience, not of necessity — see Exercise 11. However, actually splitting the two-sided improper integral into two one-sided improper integrals is, in general, necessary for getting right answers — see Exercise 12 for an example in which failing to split gives a wrong answer. For the function in Example 5, we could have used symmetry to evaluate the integral as twice the integral from `0` to `oo` — see Exercise 13.

Checkpoint 5Checkpoint 5

Go to Back One Page Go Forward One Page

Contents for Chapter 9